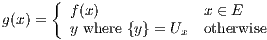Let p ∈ X, and define V n(p) to be the open ball of radius 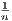 centered at p. Furthermore let Un(p) = f(V n(p)) be the
closure of f’s image of V n(p) in ℝ, and define Up to be the set ∩n=1∞Un(p). With these definitions, we obtain the
following lemmas.
centered at p. Furthermore let Un(p) = f(V n(p)) be the
closure of f’s image of V n(p) in ℝ, and define Up to be the set ∩n=1∞Un(p). With these definitions, we obtain the
following lemmas.
Lemma 1. Any finite intersection of {Un(p)} is nonempty.
Lemma 2. The set Up is nonempty.
Proof. Equation 1 implies one of two things:
-
a)
- All Un(p) are unbounded.
-
b)
- There exists an integer N such that UN(p),UN+1(p),… are bounded.
If the former is true, equation 1 implies Up is nonempty. If the latter is true, then for some integer N each Un(p)
for n ≥ N is closed (being the closure of a set) and bounded, i.e. each Un(p) for n ≥ N is compact as
they are subsets of ℝ. This fact and Lemma 1 tell us, via Rudin’s Theorem 2.36, that ∩n≥NUn(p) is
nonempty. However, due to equation 1, Up = ∩n≥NUn(p), and so Up must be nonempty in this case as
well. __
Lemma 3. The set Up contains only a single point.
Proof. For later contradiction, assume that there are distinct points x,y ∈ Up. Set ε = 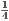 |y - x| so that, in
particular, the closure of the open ball of radius 2ε does not contain y. Since f is uniformly continuous, there
exists a δ > 0 such that any two points in E within a distance of δ of each other have that their images under f
are within a distance of ε of each other. Therefore, for integer m with
|y - x| so that, in
particular, the closure of the open ball of radius 2ε does not contain y. Since f is uniformly continuous, there
exists a δ > 0 such that any two points in E within a distance of δ of each other have that their images under f
are within a distance of ε of each other. Therefore, for integer m with 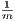 <
< 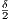 , any two points q,q′∈ V m(p)∩E
have that f(q)-f(q′) < ε. This implies, since x ∈ Up, that Um(p) ⊂B2ε(x). However, in light of our definition
of ε, this implies y ⁄∈ Um(p), which contradicts the assumption that y ∈ Up. Hence Up contains no such distinct
points x and y. Given that Lemma 2, this then implies Up must contain a single point. __
, any two points q,q′∈ V m(p)∩E
have that f(q)-f(q′) < ε. This implies, since x ∈ Up, that Um(p) ⊂B2ε(x). However, in light of our definition
of ε, this implies y ⁄∈ Um(p), which contradicts the assumption that y ∈ Up. Hence Up contains no such distinct
points x and y. Given that Lemma 2, this then implies Up must contain a single point. __
Now in light of Lemma 3, we may define a function g : X → ℝ by
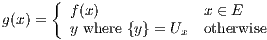
From here, I would prove continuity and uniqueness of g, but was unable to do so.
 be a metric space and f :
be a metric space and f :  → ℝ a continuous function. Denote by Z(f) the zero set of f.
These are the points p ∈
→ ℝ a continuous function. Denote by Z(f) the zero set of f.
These are the points p ∈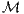 where f is zero, f(p) = 0.
where f is zero, f(p) = 0.
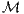 , the distance of a point p to E is defined by
, the distance of a point p to E is defined by
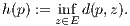
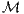 , there is a continuous function that is zero
on E and positive elsewhere.
, there is a continuous function that is zero
on E and positive elsewhere.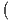

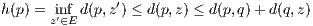
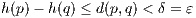
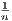 centered at
centered at 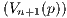
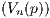 and therefore
and therefore 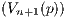
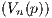
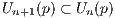
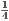
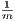
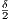 , any two points
, any two points