Math 55a: Honors Abstract Algebra
Homework 1
Lawrence Tyler Rush
<me@tylerlogic.com>
August 23, 2012
http://coursework.tylerlogic.com/math55a/homework01
I don’t know exactly why this homework’s numbers one through six are mapped to Axler’s four through fourteen in
chapter one (I assume for weighting... since those problems seem simpler than the rest), but I will make problems one
through eleven of this homework map to four through fourteen of Axler’s first chapter, and then continue on with homework
problem seven being my twelve, eight being my thirteen, etc. The title of each problem should guide anyone perfectly.
1 Axler: Chapter 1, Problem 4
Let a ∈ F and v ∈ V such that av = 0. Assume by way of contradiction that both
a≠0 and v≠0. Therefore, letting v = (v1,v2,…,vn) we have that avj = 0 for some j ∈ 1,2,…,n where vj≠0. However, this is a
contradiction with the fact that F is a field since either a or vj need to be zero but neither are. Thus we have that a = 0 or
v = 0 is true.
Replacing F with ℤ
This property will still hold for the integers.
2 Axler: Chapter 1, Problem 5
Keeping in mind that a subset of a vector space is a subspace if it
is closed under vector addition and scalar multiplication and contains 0, we need only check these three
things.
(a) Is {(x1,x2,x3) ∈ F3 : x
1 + 2x2 + 3x3 = 0} a subspace of V ?
Certainly the subset contains zero being that 0 + 2(0) + 3(0) = 0.
✓
Letting (x,y,z) and (x′,y′,z′) be in this subset, then we have that both x + 2y + 3z = 0 and x′ + 2y′ + 3z′ = 0. This results
in the following
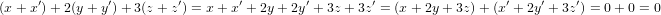
and thus the subset is closed under addition. ✓
Futhermore, letting a be a scalar in F, we can see that
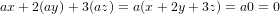
and therefore the subset is also closed under scalar multiplication. ✓
Hence we have that this subset defines a subspace of our vector space V .
(b) Is {(x1,x2,x3) ∈ F3 : x
1 + 2x2 + 3x3 = 4} a subspace of V ?
This is not a subspace since 0 + 2(0) + 3(0)≠4 and hence the subset does not
contain zero.
(c) Is {(x1,x2,x3) ∈ F3 : x
1x2x3 = 0} a subspace of V ?
This is not a subspace since we can see that (1,1,0) and (0,0,1) are in the
subset, but yet (1,1,0) + (0,0,1) = (1,1,1) would not be in the subset since 1(1)(1)≠0, and thus there is no closure under
addition.
(d) Is {(x1,x2,x3) ∈ F3 : x
1 = 5x3} a subspace of V ?
Since 0 = 5(0), then zero is contained within this subset. ✓
Letting (x,y,z) and (x′,y′,z′) be in the subset, we know that both x = 5z and x′ = 5z′, which means that the following
equation holds.
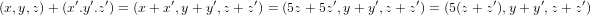
Thus the subset is closed under addition. ✓
And finally, with the following equation, letting a ∈ F3 we can see that the subset is also closed under scalar multiplication.
✓
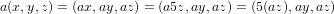
3 Axler: Chapter 1, Problem 6
The problem states that our subset needs to be nonempty, closed under addition,
and closed under taking additive inverses, which informs us that the subset of our choosing must either not include zero or
must fail to be closed under scalar multiplication. However, after a little thought about what it means to be closed
under addition and taking additive inverses informs us about the fact that zero must also be in the set (the
sum of an element and its inverse must be in the set, but what’s that?). So we are left with finding a set
where scalar multiplication is not closed. When we should multiply an element of a set by a scalar from
a field to “break” out of the set, then a discrete set should come to mind. To that end, for our example
we choose a set dealing with intgers, in fact, we will choose ℤ2, which is of course a subset of ℝ2. However
(1,1) is in the set, but 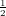 (1,1) = (
(1,1) = (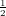 ,
,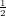 ) is not, and we now see the aforementioned “breaking” out of the
set.
) is not, and we now see the aforementioned “breaking” out of the
set.
4 Axler: Chapter 1, Problem 7
Since we only need the subset to be closed under scalar multiplication, then we
need a subset that is not closed under addition or is not closed under taking inverses. Note that multiplication of an
element by 0 ∈ ℝ will result in the zero vector, so our subset will always by default contain that element. We
know from our middle/high school mathematics experience (or at least I do) that the multiplication of two
binomials needs to be “foiled”, yielding those pesky middle terms. So we should be able to use this to our
advantage. Like the subset in problem 2c above, we use an analogous set of {(x,y) ∈ ℝ2 : xy = 0} which is closed
under scalar multiplication since axay = a2xy = 0 when xy = 0 as it would for (x,y) in this set. However,
we see that (1,0) + (0,1) = (1,1) which is not in the subset, and therefore the subset is not closed under
addition.
5 Axler: Chapter 1, Problem 8
Well certainly an intersection any amount of subspaces of V will be a subset of V ,
so thus we only need the usual zero-addition-multiplication to be satisfied. Because we have that each of the
sets in the intersection is a subspace of V , then they all contain the zero vector, and therefore, so does the
intersection. Now let x be in the intersection of subspaces, which in turn means that x is in each of the individual
subspaces and hence so is ax for any scalar a, which of course then means that the intersection contains ax as
well, and thus we have the closure of scalar multiplication on the intersection. Also let y be a vector in the
intersection. As with x above, y is also in each of the subspaces making up the intersection, and therefore, so is
their sum, x + y. Thus the sum is also in the intersection, and the intersection is therefore closed under
addition.
Replacing F with ℤ
This property will still hold for the integers.
6 Axler: Chapter 1, Problem 9
Let U1 and U2 are subspaces of V for the following proofs.
(→)
Let U1 ∪U2 be a subspace of V . Then assume by way of contradiction that neither U1 ⊆ U2 nor U2 ⊆ U1. Thus there exist
a u and u′ such that u ∈ U1, u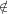 U2 and u′∈ U2, u′
U2 and u′∈ U2, u′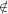 U1, which means that both u and u′ are in the union of U1 and U2.
Hence since the union is a subspace of V , then u + u′ must also be in the union. However this would mean that the sum is
also in U1 or U2, which in turn means, without loss of generality, that u + u′∈ U1. Because U1 is a vector space, then both
−u ∈ U1 and −u + u + u′ = u′∈ U1, but this contradicts the fact that u′ is not in U1, and therefore our
by-way-of-contradiction assumption is false and hence we have that either U1 is a subset of U2, or vice versa.
U1, which means that both u and u′ are in the union of U1 and U2.
Hence since the union is a subspace of V , then u + u′ must also be in the union. However this would mean that the sum is
also in U1 or U2, which in turn means, without loss of generality, that u + u′∈ U1. Because U1 is a vector space, then both
−u ∈ U1 and −u + u + u′ = u′∈ U1, but this contradicts the fact that u′ is not in U1, and therefore our
by-way-of-contradiction assumption is false and hence we have that either U1 is a subset of U2, or vice versa.
(←)
Letting U1 ⊆ U2 then we would have that U1 ∪ U2 = U2 and thus the union is also a subspace of V .
Replacing F with ℤ
This property will still hold for the integers.
7 Axler: Chapter 1, Problem 10
The subspace U + U would simply be U due to the closure of addition on U which
will demand that any element that can be constructed by the definition of the sum of vector spaces is already contained in
U.
Replacing F with ℤ
This property will still hold for the integers.
8 Axler: Chapter 1, Problem 11
The operation of addition on subspaces is both commutative and associative due
to the fact that the addition operation of vectors has both properties as well. Its pretty easy to see that if
u1 + u2 ∈ U1 + U2 then u1 + u2 = u2 + u1 ∈ U2 + U1 by the commutativity of addition, which gives us
U1 + U2 ⊆ U2 + U1. We can similarly arrive at the converse relationship to prove equivalency, and therefore the
commutativity of addition of subspaces. The proof for associativity is virtually the same as the previous
proof for commutativity, but simply replacing the commutativity of vector addition with its property of
association.
Replacing F with ℤ
This property will still hold for the integers.
9 Axler: Chapter 1, Problem 12
As we saw earlier, the operation of addition on the subspaces of V will always
have itself as an identity. Similarly, any subspace of U will be an identity for U, but note that U will not be an identity
for the subspace, outside of the trivial subspace of U itself. So we can see that the identity is not actually
unique. But this points us towards the more general idea that the addition operation of subspaces always
”expands” the subspace addends. This is due to the fact that each addend contains the zero vector, and thus
the sum of two subspaces will always have at least all the elements from the larger of the two (or more)
subspaces.
Well we know that a subspace, U, has an inverse, U−1 if U + U−1 = 0 where 0 is the identity of course. However, as a
result of what was previously discussed, there could potentially be many inverses of a subspace since there are multiple
identities for a given subspace. If we were to choose one of the trivial identities, U itself, then any subspace of U would be
the inverse of U. Although if we were to choose a subspace of U as the identity, then there would exist no subspace U−1
since it is impossible to add a subspace of U to U and have, as a result, a subspace of U. This is, of course,
unless the subspace is U. This is simply again due to the closure of the subspace addition operation, and the
“expansion” mentioned earlier in the problem; subspace adding will expand, or at the very least, result in nothing
new.
Replacing F with ℤ
This property will still hold for the integers.
10 Axler: Chapter 1, Problem 13
This seemingly looks so painfully true, but unfortunately it is not. One thing that
stumped me and made me change thoughts is that for a given u1 ∈ U1 and u2 ∈ U2 there would exist w,w′∈ W such
that
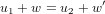
but w = w′ did not necessarily need to be true. So I began to think of previous problems (above) and specifically thought
about how adding a vector space and one of its subspaces would yield the first vector space, and then constructed the
following counter-example from knowing that.
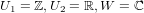
Replacing F with ℤ
This property will still hold for the integers.
11 Axler: Chapter 1, Problem 14
Let U be the subspace of 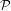 (F) consisting of all polynomials of the following
form.
(F) consisting of all polynomials of the following
form.
 | (11.1) |
Also let the subspace W of 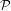 (F) consist of all polynomials of the following form.
(F) consist of all polynomials of the following form.
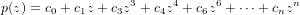 | (11.2) |
From here it is easy to see that 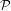 (F) = U + W since W basically “fills in” all the holes (being the powers of z) left by U to
complete the set of polynomials over F. Futhermore, since it is not possible for polynomials of the form in 11.1 to be equal
to polynomials of the form in 11.2 unless zero, then we have that the intersection of U and W must be the set containing
only {0}.
(F) = U + W since W basically “fills in” all the holes (being the powers of z) left by U to
complete the set of polynomials over F. Futhermore, since it is not possible for polynomials of the form in 11.1 to be equal
to polynomials of the form in 11.2 unless zero, then we have that the intersection of U and W must be the set containing
only {0}.
Sure this proof is slightly hand-wavy, but it is due to, in part, its innate simplicity, and also because I don’t know
of any theorem really that states that “two polynomials each with distinct powers of the input parameter
can never be equal unless all coefficients are zero”. If I knew of such a theorem, that is what I would have
used.
12 Prove That SA And SA0 Are Rings. Find The Bijection
In this proof, we let a, b, and c all be elements of SA or SA0, context will
define which one, and notation such as ak will be an element of A which belongs to the sequence a at the kth
position.
Prove SA is a ring.
Both “Abelianism” and associativity of addition on this set are proven using the same old trick of combining the
necessary elements using the definition of sum on SA, then use the definition of sum on A, and the fact that A is a ring as
well to shift around the terms of each element of SA appropriately for proving associativity or commutativity, and then
separate them again by using the inverse operation of sum on SA. These, slightly annoying, but necessary manipulations
follow first for commutativity, then associativity.
In a similar pipeline of events as above, by the following eqautions, we can easily see that the additive identity of
SA is (0,0,…) where 0 ∈ A is the identity, and also that (a0−1,a1−1,…) would be the inverse of (a0,a1,…).
The following set of equations reveal that e = (1,0,0,…) is the multiplicative identity of SA. The following set of equations shows that the product is associative on SA by showing that each term of a ∗ (b ∗ c)
is equal to the corresponding term in (a ∗ b) ∗ c. There are a few key things to notice here. The first is a
general thing about changing indicies. In a summation (∑
) there is always some fiddling that is allowed to be
done with the indicies, as long as all of the combinations “hit” in the pre-fiddling from are the same as the
post-fiddling form, and sometimes it is only the NUMBER of combinations that matter, but that is a discussion for
another time. Nonetheless this property is only true for summations when the sum is a commutative operation,
and since we are in the world of a ring, A, we are free to switch around indicies! So we take advantage of
this in the changes from equation 12.4 to equation 12.5 and also from equation 12.6 to equation 12.7. The
other thing to note is that the distributive law of A allowed us to go from equation 12.5 to equation 12.6.
Like above, the following equations yield that each term of a(b + c) is equal to the corresponding term in ab + ac. Giving to
us that the distributive law holds for SA, and thereby satisfying our final property to prove that SA is a ring.
Prove that SA0 is a ring.
Here, like subspaces, we just need to check that SA0 contains both sum and product identities and is closed under both
of the sum and product operations. Since the sum identity is all zeros, and the multiplicative identity is a one followed by
all zeros, then they are both contained in SA0. The set is closed under addition since the addition of a and b is pairwise and
the result, say r, will be such that rn = 0 for all n > max(na,nb) where na and nb are such that ai = 0 and bj = 0 for all
i > na and j > nb.
Find an isomorphism from A to SA0.
Here we need to find an isomorphism. I like to believe I have a knack for finding them, and it seems like that is really the
only method. However, I can say that there are two things that seem to pop up time-after-time for me whenever I am
tasked with finding a isomorphisms or, more generally, bijections. First, keep it simple. For some reasons a lot of
isomorphisms that I have seen are not that complicated, and they always seem to ”make sense”. Second, there for some
reason seems to be nice symmetries involved in a lot of isomorphisms/bijections, especially ones that can be shown
pictorially.
Anyway, to get back to business, the mapping here is the following for a ∈ A.
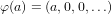
Instantly we can easily see that this mapping takes both the sum and product identities to the sum and product
identities in SA0. Likewise the fact that additive inverses are taken to additive inverses are just as simple to see.
Also by the following set of equations we have that this mapping preserves the sum structure of A in SA0
and here, the product structure. Now assume that φ(a)≠φ(b). Therefore (a,0,0,…)≠(b,0,0,…), which guarentees us that a≠b, and hence we know that
our homomorphism is one-to-one. Since we are only trying to prove that there exists a set, inside of SA0
i.e. a subset, with structure identical to that of A, but not one in particular, then we don’t care about the
homomorphism being onto since the image of the mapping will simply act as our subset and mappings are, by
definition, onto their own images. Hence we have that there is indeed a subset of SA0 that is isomorphic to
A.
13 The Commutativity and “(Integral Domain)-ness” of SA and
SA0
Let the initial assumptions from the previous problems be the same for this
problem.
(a) Prove SA and SA0 are commutative iff A is too.
Let SA and SA0 be commutative rings. Since we know that there exists a
isomorphic version of A in these rings, as proven in the previous problems, then we can use that isomorphism to help us
out. Thus the following equations give us that A is commutative.
Conversely, assume that A is a commutative ring. Then the following set of equations hold.
Hence we have that the nth term of a ∗ b is equal to the nth term of b ∗ a, and thus both SA and SA0 are
commutative.
(b) Prove SA and SA0 are integral domains iff A is too.
Assume that SA is an integral domain. Thus for some x,y ∈ A each of which
are non-zero, we have that φ(x) and φ(y), where φ is the isomorphism from A into SA, are both non-zero since only zero
maps to zero. Therefore the product φ(x)φ(y) is non-zero because SA is an integral domain. This in turn
means that φ−1(φ(x)φ(y)) is also non-zero, again because only zero maps to zero. Hence, because we have
that
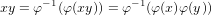
then xy is also non-zero. Thus A is an integral domain.
Conversely, assume that A is an integral domain. Assume by way of contradiction that SA is not an integral domain.
Therefore there exists an a,b ∈ SA with a≠0 and b≠0 such that ab = 0. Let indicies j and k be such that aj≠0 and am = 0
for all m < j. Allow the same for b and k as is for a and j, respectively. Without loss of generality, let j be less than k.
Therefore, since the nth term of ab is
 | (13.11) |
then we have that ajbk will be a term in the summation in (ab)k+j. Because a0 = a1 =  = aj−1 = 0 and
b0 = b1 =
= aj−1 = 0 and
b0 = b1 = 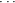 = bk−1 = 0, then, given the indices of convolution (equation 13.11), ajbk is the only term in the summation
defining (ab)k+j where neither of the operands is zero. Thus we have that (ab)k+j = ajbk, and since ab = 0 then aj and bk
are zero divisors of A, since neither are zero, but this is a contradiction of the fact that A is an integral domain and thusly
has no zero divisors. Hence SA must be an integral domain. Note that this proof applies without change to SA0 as
well.
= bk−1 = 0, then, given the indices of convolution (equation 13.11), ajbk is the only term in the summation
defining (ab)k+j where neither of the operands is zero. Thus we have that (ab)k+j = ajbk, and since ab = 0 then aj and bk
are zero divisors of A, since neither are zero, but this is a contradiction of the fact that A is an integral domain and thusly
has no zero divisors. Hence SA must be an integral domain. Note that this proof applies without change to SA0 as
well.
14 Prove that if A is a field, than neither SA nor SA0 are. Give a simple
description of the invertible elements of each.
This one seems like it shouldn’t be that hard. We have already shown that for any
property of a field save for multiplicative inverses, if A has such a property, than SA and SA0 do as well, so we know that it
is the multiplicative inverses that fail that neither SA nor SA0 are a field when A is one. However, I just can’t quite figure
out the reason why.
15 “Two-sided” sequence consequence.
16 An electoral college computation example.
References
[1] Artin, Michael. Algebra. Prentice Hall. Upper Saddle River NJ: 1991.
[2] Axler, Sheldon. Linear Algebra Done Right 2nd Ed. Springer. New York NY: 1997.
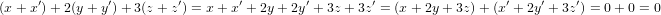
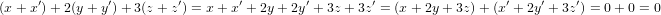
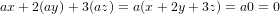
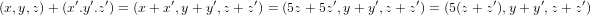
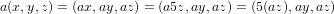
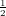 (1,1) = (
(1,1) = (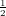 ,
,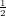 ) is not, and we now see the aforementioned “breaking” out of the
set.
) is not, and we now see the aforementioned “breaking” out of the
set.
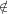 U2 and u′∈ U2, u′
U2 and u′∈ U2, u′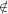 U1, which means that both u and u′ are in the union of U1 and U2.
Hence since the union is a subspace of V , then u + u′ must also be in the union. However this would mean that the sum is
also in U1 or U2, which in turn means, without loss of generality, that u + u′∈ U1. Because U1 is a vector space, then both
−u ∈ U1 and −u + u + u′ = u′∈ U1, but this contradicts the fact that u′ is not in U1, and therefore our
by-way-of-contradiction assumption is false and hence we have that either U1 is a subset of U2, or vice versa.
U1, which means that both u and u′ are in the union of U1 and U2.
Hence since the union is a subspace of V , then u + u′ must also be in the union. However this would mean that the sum is
also in U1 or U2, which in turn means, without loss of generality, that u + u′∈ U1. Because U1 is a vector space, then both
−u ∈ U1 and −u + u + u′ = u′∈ U1, but this contradicts the fact that u′ is not in U1, and therefore our
by-way-of-contradiction assumption is false and hence we have that either U1 is a subset of U2, or vice versa.
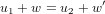
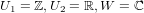
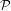 (F) consisting of all polynomials of the following
form.
(F) consisting of all polynomials of the following
form.

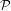 (F) consist of all polynomials of the following form.
(F) consist of all polynomials of the following form.
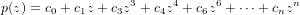
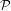 (F) = U + W since W basically “fills in” all the holes (being the powers of z) left by U to
complete the set of polynomials over F. Futhermore, since it is not possible for polynomials of the form in 11.1 to be equal
to polynomials of the form in 11.2 unless zero, then we have that the intersection of U and W must be the set containing
only {0}.
(F) = U + W since W basically “fills in” all the holes (being the powers of z) left by U to
complete the set of polynomials over F. Futhermore, since it is not possible for polynomials of the form in 11.1 to be equal
to polynomials of the form in 11.2 unless zero, then we have that the intersection of U and W must be the set containing
only {0}.
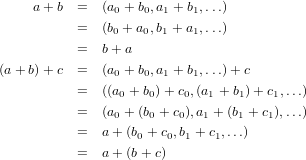
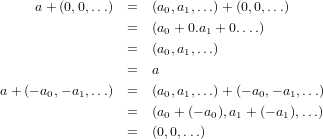
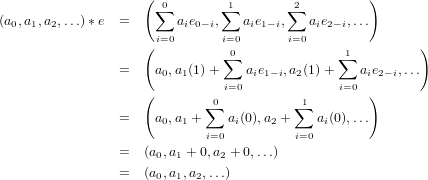
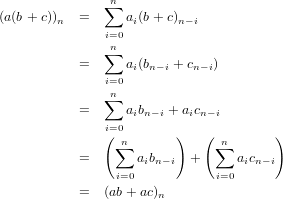
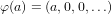
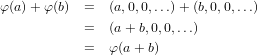
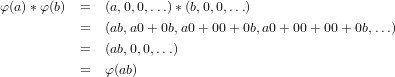
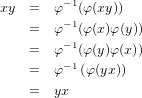
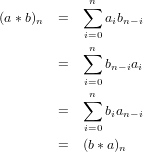
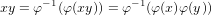

 = aj−1 = 0 and
b0 = b1 =
= aj−1 = 0 and
b0 = b1 = 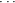 = bk−1 = 0, then, given the indices of convolution (equation 13.11), ajbk is the only term in the summation
defining (ab)k+j where neither of the operands is zero. Thus we have that (ab)k+j = ajbk, and since ab = 0 then aj and bk
are zero divisors of A, since neither are zero, but this is a contradiction of the fact that A is an integral domain and thusly
has no zero divisors. Hence SA must be an integral domain. Note that this proof applies without change to SA0 as
well.
= bk−1 = 0, then, given the indices of convolution (equation 13.11), ajbk is the only term in the summation
defining (ab)k+j where neither of the operands is zero. Thus we have that (ab)k+j = ajbk, and since ab = 0 then aj and bk
are zero divisors of A, since neither are zero, but this is a contradiction of the fact that A is an integral domain and thusly
has no zero divisors. Hence SA must be an integral domain. Note that this proof applies without change to SA0 as
well.