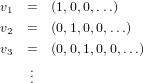
1 Exercise 7 On Page 35 Of Axler; From That, Deduce Exercises 5 And 6
Exercise seven’s proof. Assume that we have a sequence of vectors, v1,v2,… such that (v1,v2,…,vn) is linearly independent for all positive integers n. In Artin, we see that a finite set of vectors that spans V must be at least as large as any set of vectors that is linearly independent [1, pg 92]. Hence we can see that because we are gaurenteed to have an arbitrarily large, finite set of linearly independent vectors, then there exists no finite set of vectors that spans V , i.e. no LIST of vectors that spans V . Thus the space if infinite-dimensional.
For the reverse direction, if our vector space V is infinite-dimensional, then there exists no list of vectors that spans the space. Hence, we can find a linearly independent set of vectors in the space, call it L. We know they exist! The space is infinite-dimensional and any one non-zero vector will make a linearly independent set! Since we know that span(L)≠V , then we can find a vector in V that is not in span(L), call this v′. Thus the set L ∪{v′} will also be linearly independent. Continuing this pattern allows us to create a linearly independent set of vectors of any size, i.e. there exists a sequence of vectors v1,v2,… such that (v1,v2,…,vn) is linearly independent for all positive integers n.
Deduce exercise five’s result from the above proof. To deduce five from the above result, we need to find an infinite sequence of linearly independent vectors. Hence we can take a page out of the standard basis’ book with the following set of vectors.
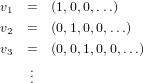
Deduce exercise six’s result from the initial proof. Now we need to find another sequence of linearly independent vectors. Hence we go in with the “simple” mindset and can discover the following infinite sequence of linearly independent vectors.
2 Give the dimensions of the vector spaces generated by each of the following sets of vectors.
(a) The vectors (1,i, 1 + i, 0), (−i, 1, 1 − i, 0), and (1 − i, 1 + i, 2, 0) in ℂ4

Similarly, we can see that the third vector is a multiple of the first.

(b) The functions f(x) = sin x, sin(x + π∕6), and sin(x + π∕3) in ℝℝ
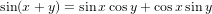
we can obtain these two forms for sin(x + π∕3) and sin(x + π∕6) equations.
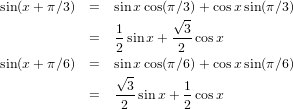
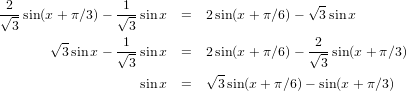
So at most, the dimension of the spanning set of this set of vectors is two. However, because sin(x + π∕3) is not a scalar multiple of sin(x + π∕6), we can conclude that the dimension of the span of this set of vectors can not be one either, leaving us with a dimension of two.
(c) The n vectors given in the homework description (nope, not writing them out)
3 Give a basis for the specified subspaces.
(a) The subspace {x→ : x
1 + x2 +  + xn = 0} in Fn
+ xn = 0} in Fn
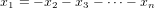
indicating that all vectors in the space have the following form.
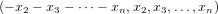 | (3.1) |
This gives us a nice way to derive a spanning set, and as well see, also an independent one. We can break down the vector in equation 3.1 as a sum of n − 1 vectors giving us a spanning set for the subspace. The break-down is as follows.
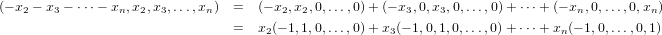
 + (−1,0,…,0,1) is linearly
independent.
+ (−1,0,…,0,1) is linearly
independent.
(b) The subspace V = {P : P(−3) = 0} of 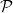
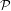 comes to mind. So we
start our meddling there. We need each polynomial in the standard basis to be zero on input of −3, hence
we account for that by subtracting (−3)n from each xn in the standard basis to obtain the following set of
vectors.
comes to mind. So we
start our meddling there. We need each polynomial in the standard basis to be zero on input of −3, hence
we account for that by subtracting (−3)n from each xn in the standard basis to obtain the following set of
vectors.
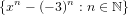 | (3.2) |
Its easy to see that this set is linearly independent since no linear combination of any elements in the set will result in the necessary exponential of x to be equivalent to another element of the set.
Assume, by way of contradiction, that the set specified in 3.2 does not span V . Therefore there exists some polynomial,
p(x) = a0 + a1x1 + a2x2 +  + anxn, such that p(−3) = 0 but p(x)
+ anxn, such that p(−3) = 0 but p(x)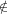 span({xn − (−3)n : n ∈ ℕ}). Thus we have
that
span({xn − (−3)n : n ∈ ℕ}). Thus we have
that
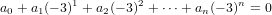
which in turn demands the following.
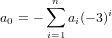
Hence we have that
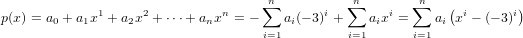
which implies that p(x) is indeed in the span of the set in 3.2. This is the contradiction of our above assumption and therefore the set {xn − (−3)n : n ∈ ℕ} is a basis for V .
Assume that for any n elements, p1,p2,…,pn in F, there exists a unique polynomial q ∈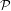 (F) of degree less than n such
that q(ai) = pi for all i = 1,2,…,n. Letting c1,c2,…,cn be the coefficients of q, then
(F) of degree less than n such
that q(ai) = pi for all i = 1,2,…,n. Letting c1,c2,…,cn be the coefficients of q, then
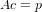
where c is the vector of coefficients of q, p = (p1,p2,…,pn, and A is an n×n matrix such that the ith row is the ith vector of the set vi := (a1i,a2i,…,ani) (taking rows to be indexed initially at 0). Since this UNIQUE equation is ALWAYS true for ALL possible vectors p in Fn, then the above assumption is akin to assuming that the rows of A are a basis for Fn, which certainly implies that the set of vectors vi := (a1i,a2i,…,ani) are linearly independent.
Conversely, assume that the n vectors vi := (a1i,a2i,…,ani) with (0 ≤ i < n) in Fn are linearly independent. Therefore we have that the this set of vectors is also a basis for Fn, given the number of vectors. Hence EVERY vector (p1,p2,…,pn) in Fn has a unique respresentation of the form
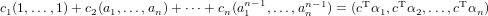
where c = (c1,c2,…,cn) and αi = (1,ai,ai2,…,ain−1). Therefore if we construct a polynomial in 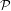 (F)
(F)
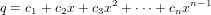
then q would be a polynomial of degree less than n such that for all p1,p2,…,pn ∈ F q is the unqiue polynomial such that q(ai) = pi for all i = 1,2,…,n.
5 Complexification of a real vector space
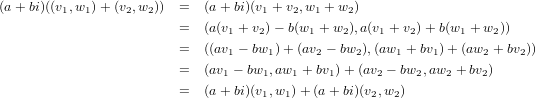
If V is finite-dimensional, then V C would have the same dimension as the V ⊕ V direct product, i.e. 2dim(V ).
6 Dimension of K-vector spaces in F
As for the number of ordered bases, each such basis is made up of n linearly independent vectors since V = Fn has
dimension n. So we’ll proceed by counting to find the number of lists (i.e order matters) of independent vectors of size n.
The number of lists of linearly independent vectors of size one is simply the number of nonzero vectors, qn − 1. To obtain a
list of two linerarly independent vectors, we pick a second vector outside of the span of the first; note that this vector will be
nonzero as the zero vector is contained within the span of any set of vectors. Since the span of the first vector has size q (i.e.
the total number of linear combinations, since each linear combination is a unique vector since the vectors are
linearly independent), then our number of choices for the second is qn − q. This gives us (qn − 1)(qn − q) lists
of linearly independent vectors of size two. Since the span of two linearly independent vectors would have
size q2, our choices for a third vector are limitied to qn − q2 vectors giving us (qn − 1)(qn − q)(qn − q2)
linearly independent lists of size three. So finally, to add a kth linearly independent vector to a list of k − 1
linearly independent vectors, we would have qn − qk−1 choices, yielding (qn − 1)(qn − q)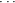 (qn − qk−1) linearly
independent lists of size k. Thus when k = n the list will be a basis, and therefore the number of ordered bases
is
(qn − qk−1) linearly
independent lists of size k. Thus when k = n the list will be a basis, and therefore the number of ordered bases
is
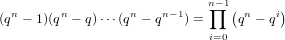
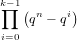
however, this counts different orderings of the k vectors, which matters not as different orderings of the same vectors results in identical subspaces. So we must divide out by the number of orderings of the k vectors. This leaves us with
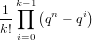
M[n] is a subgroup. Let a and b be n-torsion elements of M. Then we have that n(a + b) = na + nb = 0 + 0 = 0, and thus M[n] is closed. Since n0 = 0 then M[n] contains the identity element. Finally since (n − 1)a + a = (n − 1 + 1)a = na = 0, a + (n− 1)a = (1 + n− 1)a = na = a, and n((n− 1)a) = (n− 1)na = (n− 1)0 = 0, then each element of M[n] has its inverse in M[n].
Mtors is a subgroup. Letting a,b ∈ Mtors we know that there exists integers na and nb such that naa = 0 and nbb = 0. Given this, we have nanb(a + b) = nanba + nanbb = nbnaa + na0 = nb0 = 0, so Mtors is closed. Again, since any integer times the identity of M will result in the identity of M, then it is in Mtors. As proven in the previous paragraph, the inverse of a torsion element will be in the same n-torsion subgroup as the torsion element itself, which implies that Mtors is closed for inverses. Therefore Mtors is a subgroup of M.
(i) Non-trivial Divisible Group
[1] Artin, Michael. Algebra. Prentice Hall. Upper Saddle River NJ: 1991.
[2] Axler, Sheldon. Linear Algebra Done Right 2nd Ed. Springer. New York NY: 1997.
[3] Valdex-Sanchez, Luis. Table of Trigonometric Identities Last Edited: December 3, 1996. Available at: http://www.sosmath.com/trig/Trig5/trig5/trig5.html