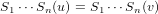
Fine, I’ll give-in to the numbering system this time.
1 Implications of Spanning Set Countability
(a) Prove a vector space over a countable field that has a countable spanning set is countable as well.
(b) Prove that any vector space with a countable spanning set over any field does not have an uncountable linearly independent set.
2 Implications of Vector Space Countability on Spanning Sets
3 Problems 6 and 22 of Axler’s Third
Sn is itself
a mapping from, say V , to some arbitrary vector space. Therefore, if we have that
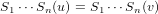
for some vectors u,v ∈ V , then by injective property of S1 we also have the following.
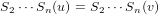
Likewise by S2’s property of injection we also have that
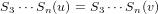
and so on, until the continuation of this pattern arrives at the final implication that u = v. Hence S1
Sn is an
injection.
If S1
Sn is injective, what can be said about each individual mapping?
Each individual mapping is also injective in this case.
Assume that S1
Sn is an injective mapping with some vector space V as its domain. Let S1
Sn(u) = S1
Sn(v) for
some u,v ∈ V . From which we know that u = v by the injective property of S1
Sn. Thus we have that
Sn(u) = Sn(v) is also true, which in turn implies that that S1
Sn-1 is injective. We can continue with
this sequence of “if-this-than-that” n - 1 more times, arriving at the final conclusion that the mappings
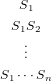
Now assume that Si(u′) = Si(v′) for i ∈{1,…,n} and some vectors u′,v′ in the domain of Si. Therefore we have that
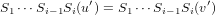
which, by the above result, implies that u′ = v′. Hence Si is an injective mapping, and subsequently, so are all the mappings S1,…,Sn.
(V ) are such that ST is
invertible. Let T(u) = T(v) for some vectors u,v ∈ V . Therefore, ST(u) = ST(v) which implies that u = v
since ST is an injection. Thus T is also an injection. Hence the by Axler’s Theorem 3.21 [2, pg 57], T is
invertible.
In a similar manner, if we now assume that S(u) = S(v) then there exists a u′,v′∈ V such that ST(u′) = S(u) = S(v) = ST(v′), by T’s surjectivity. Hence because ST is injective then u′ = v′, which indicates that u = v since T is a bijection for which T(u′) = u and T(v′) = v are true. Thus S is an injection, for which Axler’s Theorem 3.21 [2, pg 57] yields to us that S is indeed invertible.
For the opposite direction, assume that S and T are each, individually, invertible mappings. From the solution to Axler’s problem six in chapter three (above) we learned that ST is therefore an injection. Thus, again using Axler’s Theorem 3.21 [2, pg 57], we have that ST too is invertible.
4 Problems 23 and 24 of Axler’s Third
(V ). Then assuming that we have ST = I then the following
equation holds for some v ∈ V .
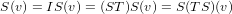
Hence TS = I. The other direction is similarly proven by this proof due to symmetry.1
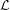(V ) is a scalar multiple of the identity
tranformation on 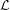(V ). Let this scalar be a. Hence for all S ∈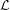(V ) the following equation holds for some
v ∈ V .
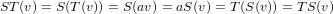
Therefore we can see that ST = TS.
5 Polynomials on ℝ and ℂ Vector Spaces
(a) Show that the evaluation map is a linear transformation.
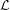(V,W) and v ∈ V .
With the following, we have homogeneity for some a in the field over which V and W lie.
Hence the evaluation map is a linear transformation.
To aide in our proof let us first prove homogeneity when over Z. So assume that n ∈ ℤ. Then we have
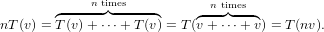 | (7.1) |
Now let q = 
∈ ℚ. Using equation 7.1 and a small trick, we get the following.
Thus we have that T is linear.
8 Existence of Unique Dual Bases
Anyways, I realized after goin through the problem that if I just would have applied the “Kronecker-delta” result itself,
the UNIQUE basis would have directly revealed itself.
Assume that V is a finite-dimensional vector space with v1,…,vn as its basis, and that V * the vector space of linear maps
from V to F, where F is the field over which V lies.
The existence and uniqueness of “Kronecker Maps” Let the mapping vj* in V *i for 1 through n be such that, for all v,
then its easy to see that the jth of these mappings will each for the Kronecker map for each of the vectors in the basis of V mentioned above.
Assume by way of contradiction that for at least one j, vj* is not unique, taking ej ∈ V * to be one such mapping with ej≠vj* but ej(vi) = δij for the basis, v1,…,vn. Therefore we have the following set of equations for each v ∈ V .
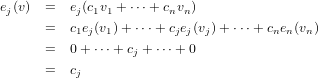
These maps are a basis for the dual space V *. By the following sequence of equations for an arbitrary vector, e, in the dual space of V , we have that v1*,…,vn* spans V *, if we let e(vi) = ci′ for each i of the indicies of the basis of V .
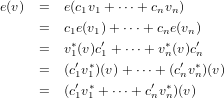
Assume by way of contradiction that this set of vectors in the dual space is not linearly independent. Thus, at the very least, one of these vectors is a linear combination of the others. Let this said vector be vi*, which therefore implies that
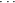+ cnvn ∈ V . However, this leads to the following set of equations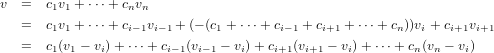 
9 Dual of Direct Sum of Multiple Vector Spaces
This in turn yields to us the following.
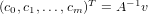
Since the columns of A form a basis, by construction, then we know that it is invertible and that A-1 exists. Hence we can finally see that
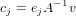
where ej is simply the jth vector of the standard basis. Thus we are left to concluded that the jth element of the dual basis of Fm+1 is nothing more than the operation induced by multiplication by ejA-1.