
(i) Points and lines in
Let U1 and U2 be distinct “points” of the projective space PV . Because they’re distinct, then their intersection is simply the zero vector since they are each one dimensional. This gives us

So any subspace W containing both U1 and U2 will have dimension of at least 2, since it will necesarily contain U1 + U2. In particular if W has dimension 2, then W is the space U1 + U2, and so the unique line containing both U1 and U2 is U1 + U2.
Let U1 and U2 be distinct lines both contained in some projective plane, say W. Being lines, dimU1 = dimU2 = 2, but since they are distinct then dim(U1 + U2) > 2. Now since dimW = 3, then dim(U1 + U3) ≤ 3 and therefore dim(U1 + U2) is squeezed to be 3. Thus we have
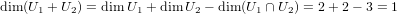
and therfore U1 ∩ U2 is a point.
2 Axler: Chapter 5, Exercise 4
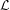 (V ) are such that ST = TS. Prove
that ker(T - λI) is invariant under S for every λ ∈ F.
(V ) are such that ST = TS. Prove
that ker(T - λI) is invariant under S for every λ ∈ F.
Problem Solution. Let v be in the kernel of T - λI. Therefore we have that for any v ∈ ker(T - λI),
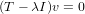
Applying S to both sides of the above equation yields the following sequence.
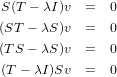
3 Axler: Chapter 5, Exercise 7
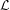 (Fn) is defined
by
(Fn) is defined
by
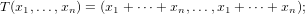
in other words, T is the operator whose matrix (with respect to the standard basis) consists of all 1’s. Find all eigenvalues and eigenvectors of T.
Problem Solution. If (x1,…,xn) were to be an eigenvector of T, then it must have the property that
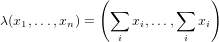
indicating that each xj is 1∕λ of the sum of all the elements comprising the vector. Hence all eigenvectors of T must be of the form (x,…,x).
4 Axler: Chapter 5, Exercise 8
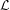 (F∞) defined by
(F∞) defined by
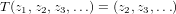
Problem Solution. The eigenvectors are such that

where λ is a possible eigenvector of T. Thus we have that z2 = z1λ, z3 = z2λ, z4 = z3λ,…; meaning that the ith element of every eigenvector corresponding to an eigenvalue, λ, of T is of the following form.
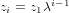
Thus the an eigenvector of T is going to be a vector whose terms are the terms of a geometric progression, and associated eigenvalue is going to be the multiplier (or as wikipedia tells me, the “common ratio”) of the said progression.
5 Axler: Chapter 5, Exercise 9
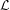 (V ) and dim(T(V )) = k. Prove that T
has at most k + 1 distinct eigenvalues.
(V ) and dim(T(V )) = k. Prove that T
has at most k + 1 distinct eigenvalues.
Problem Solution. Since the dimension of the image of T is k, then there is no linearly independent set of vectors of size larger than k in the image. Since eigenvectors for a given eigenvalue have the form
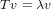
then all vectors in a given set of eigenvectors corresponding to distinct eigenvalues will be in the image of T, and thus limited in size to k, which in turn limits the number of such eigenvectors to k. Those eigenvalues, however, would be non-zero, thus throwing in with them, the eigenvalue zero, we get that the number of distinct eigenvalues is limited to k + 1 (note that only non-zero eigenvalue have eigenvectors in the image, and not in the kernel).
6 Axler: Chapter 5, Exercise 10
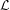 (V ) is invertible and λ ∈ F \{0}. Provethat
λ is an eigenvalue of T if and only if 1∕λ is an eigenvalue of T-1.
(V ) is invertible and λ ∈ F \{0}. Provethat
λ is an eigenvalue of T if and only if 1∕λ is an eigenvalue of T-1.
Problem Solution.
Let T ∈ (V ) be an invertible mapping and, a nonzero, λ ∈ F be an eigenvalue of T. Let v be an eigenvector for
corresponding to λ. In this case we have the following.
(V ) be an invertible mapping and, a nonzero, λ ∈ F be an eigenvalue of T. Let v be an eigenvector for
corresponding to λ. In this case we have the following.
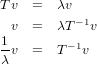
7 Axler: Chapter 5, Exercise 11
 (V ). Prove that ST and TS have the same
eignevalues.
(V ). Prove that ST and TS have the same
eignevalues.
Problem Solution. Let λ be an eigenvalue of ST. Then there exists a v ∈ V such that STv = λv. Multiplying both sides by T we get
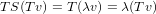
and thefore λ is also an eigenvalue for TS.
8 Axler: Chapter 5, Exercise 12
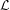 (V ) is such that every vector in V is
an eigenvector of T. Prove that T is just a scalar multiple of the identity operator.
(V ) is such that every vector in V is
an eigenvector of T. Prove that T is just a scalar multiple of the identity operator.
Problem Solution. I don’t know how to prove this for infinite dimensional vector spaces, so assuming finite dimensional, we1 We have that for v ∈ V with eigenvalue λ where dimV = n and λ1,…,λn, which may or may not be distinct, are the eigenvalues for some basis v1,…,vn.
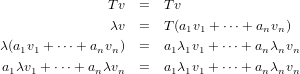
9 Axler: Chapter 5, Exercise 15
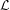 (V ), p ∈ P(C), and a ∈ C. Prove
that a is an eigenvalue of p(T) if and only if a = p(λ) for some eigenvalue λ of T.
(V ), p ∈ P(C), and a ∈ C. Prove
that a is an eigenvalue of p(T) if and only if a = p(λ) for some eigenvalue λ of T.
Problem Solution. Let a = p(λ) be an eigenvalue of p(T). Thus there exists some vector v such that
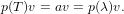
This indicates that

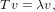
and λ is an eigenvalue of T.
Conversely if we suppose that λ is an eigenvalue of T, then there is a vector v such that
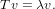
Thus applying p(T) to v we get the following.
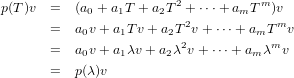
10 Axler: Chapter 5, Exercise 16
11 Axler: Chapter 5, Exercise 21
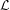 (V ) and P2 = P. Prove that
V = kerP ⊕ P(V ).
(V ) and P2 = P. Prove that
V = kerP ⊕ P(V ).
Problem Solution. 2 Let us refer to kerP ⊕ P(V ) as W. Assume by way of contradiction that V is not W. We know that W is a subspace of V since both the image and the kernel of P are subspaces of V , which implies, by our assumption, that V is not a subspace of W. Thus there exists at least one basis vector of V that is not in W. Let v′ be such a basis vector, and allow vk1,…,vk2 and vi1,…,vi2 to be the basis vectors of the kernal and the image of P, respectively.
Since v′ is outside of the kernel of P, then Pv′ is representable as a linear combination of vi1,…,vi2 and since P2 = P, then
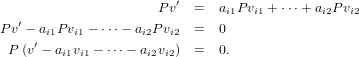
 - ai2vi2 is in the kernel of P. Thus we in turn have the following,
- ai2vi2 is in the kernel of P. Thus we in turn have the following, 
12 Finding eigenvalues and eigenvectors.

which, seeing as we “don’t know” about determinents yet, we will attack by brute force. Solve the equation
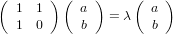
for λ and hope we get something good in return. Alas, we get the following two equations
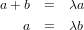
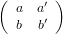
where (a b)T and (a′ b′)T are eigenvectors corresponding to φ+ and φ-, respectively, will be invertible according to Artin [1, pg 96]. Continuing this run of “furthermores” and “hences”, we thus have that A has a diagonal matrix with respect to the basis of its eigenvectors, as per Axler [2, pg 88-89].
Let’s let b of the eigenvectors (a b)T be 1 for both eigenvectors corresponding to φ+ and φ-. Hence our eigenvectors are

Saving you the eye-sore of a calulation that is finding the inverse of
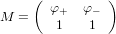 | (12.1) |
via the stick-the-identity-matrix-on-the-right-and-convert-to-rref method, we have that M has
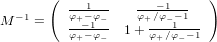
as an inverse. Man that’s nasty.3
Now we have M-1AM will be a diagonal matrix equal to
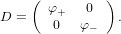
Thus we can write a closed form expression of At by MDtM-1, or in a way more conducive to understanding the computational simplicity,
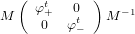
See the appendix for the Octave output showing the differences between the one form and the other.
[1] Artin, Michael. Algebra. Prentice Hall. Upper Saddle River NJ: 1991.
[2] Axler, Sheldon. Linear Algebra Done Right 2nd Ed. Springer. New York NY: 1997.
We see below that all of the answers turn out to be the same whether calculating At directly or by using its representation in the basis of it’s eigenvectors.