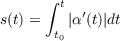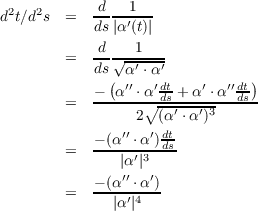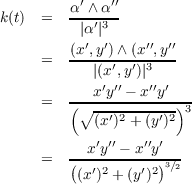Math 501: Differential Geometry
Homework 1
Lawrence Tyler Rush
<me@tylerlogic.com>
January 26, 2013
http://coursework.tylerlogic.com/courses/math501/homework01
1 do Carmo pg. 5 exercise 2
Assume for later contradiction that α′(t0) is not orthogonal to α(t0). Since α′(t0)
is nonzero, then we are able to find a ϵ > 0 such that either |α(t0 -ϵ)| < |α(t0)| or |α(t0 + ϵ)| < |α(t0)|. However, either case
contradicts the fact that α(t0) is the point of the trace of α which is closest to the origin. Thus α′(t0)⊥α(t0) must be
true.
2 do Carmo pg. 7 exercise 2
(a)
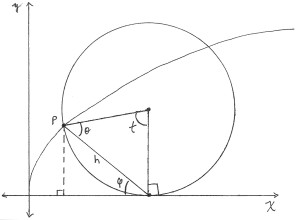
We will parametrize the cycloid by the angle of rotation, denote it by t. From
the diagram in Figure 1 it can be seen that Thus the value of h is determined by the following sequence of equations. With these things, we can finally derive the point p. and
(b)
Let’s rotate from 0 to 2π, fixing t0 at 0. By making use of the double angle
formula for cos, we have the following.
3 do Carmo pg. 7 exercise 3
(a)
For this problem we will use Figure 2 as a guide. Using some trigonometry,
from the figure we get the following (remember the diameter is length 2a) These allow us to have the following Hence letting t = tanθ we get

(b)
Because
then α(0) = (0,0), and so α has a singular point at the origin (0,0).
(c)
4 do Carmo pg. 11 exercise 10
(a)
Left Equation
For α(t) = (x(t),y(t),z(t)) the Fundamental Theorem of Calculus gives us that there is a c ∈ I such
that
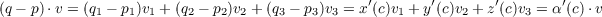
but since v is a vector of magnitude 1, then
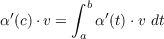
so
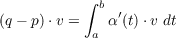
Right Inequality
By the definition of dot product
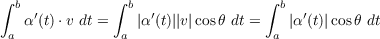
Now since cosθ ranges between -1 and 1 then
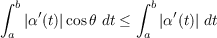
(b)
5
(a)
To show that α(t) is parametrized by arc lenght, we must show |α′(t)| = 1 for
all t. So proceeding that way, we have giving us
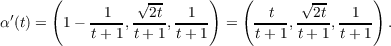
Therefore |α′(t)| is
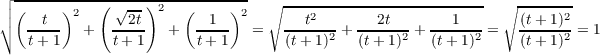
Hence α is parametrized by arc length.
(b)
Curvature.
The curvature, κ, is |α′′(t)|. Using what we know from the previous part,
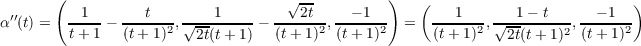
then
Torsion.
The torsion of α, τ, is the magnitude of the derivative of the binormal vector, b, as given by the Frenet equation b′ = τn.
The binomial vector is
so and thus
6 do Carmo pg. 22 exercise 1
The following are for
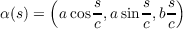
(a) The parameter s is the arc length
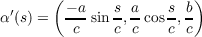

Therefore s is the arc length.
(b) Curvature and torsion.
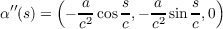


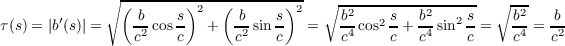
(c)
The osculating plane of α at s = s0 is defined by the following point, normal
vector tuple

the equations for which are given and determined in the previous problem.
(d)
The angle between the z-axis and a line passing through α(s)
and containing n(s) will be the same as the angle between n(s) and any vector contain by the z-axis, say
(0,0,1). And that angle will be the inverse cosine of their dot product, since both vectors have magnitude of
one.
Since n(s)(k(s))-1α′′(s) = 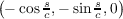 , then the dot product of it and (0,0,1) is zero, implying
that the cosine of the angle between them is zero, which in turn confirms that the angle between them is
, then the dot product of it and (0,0,1) is zero, implying
that the cosine of the angle between them is zero, which in turn confirms that the angle between them is
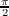 .
.
(e)
This is similar to the previous problem except that we will use t(s) in place of
n(s). Because

i.e. the cosine of the angle between them is a constant, then the angle bewteen t and (0,0,1) is constant, since they both
have a magnitude of one.
7 do Carmo pg. 25 exercise 12
(a)
Since
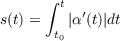
then by the fundamental theorem of calculus we have ds∕dt = |α′(t)|, which implies dt∕ds = 1∕|α′(t)|.
Taking the derivative of both sides of the above equation leads to the following sequence of equations.
(b)
(c)
(d)
Assuming that the yet-to-be-proven part (b) of this problem is true, then the
signed curvature is
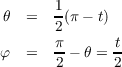
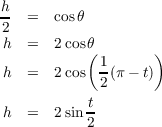
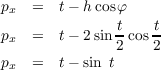

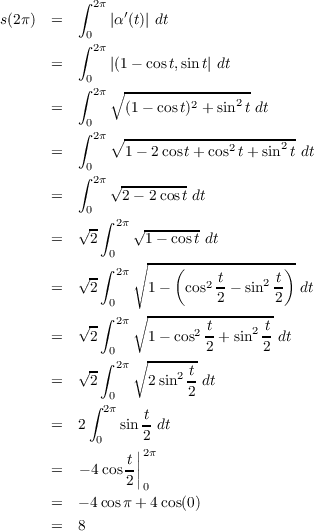
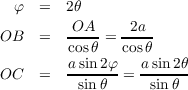


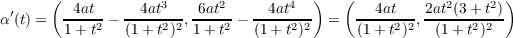
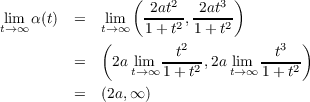
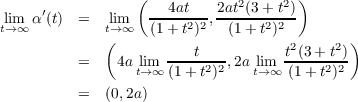
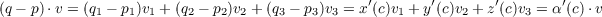
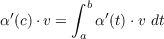
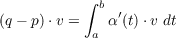
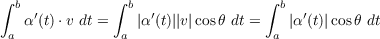
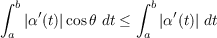
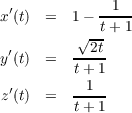
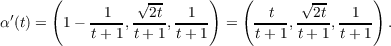
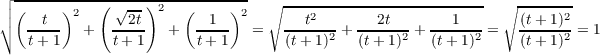
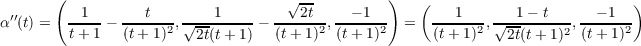
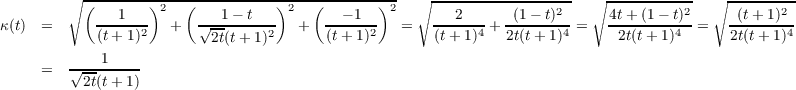
![b(t) = t(t′)∧ n(t) - ′′
b(t) = α( (t)∧ (κ(t)) 1α (t))
t √2t- 1 √ -- ( 1 1- t - 1 )
b(t) = t+-1,t+-1,t+-1 ∧ 2t(t+ 1) (t+-1)2,√2t(t+-1)2,(t+-1)2-
( √ -- ) ( √ -- √--)
-t-- --2t --1- --2t 1--t ---2t
b(t) = t+ 1,t+ 1,t+ 1 ∧ t+ 1,t+ 1, t+ 1
[( √-- ) (√ -- √ --)]
b(t) = ---1--2 t, 2t,1 ∧ 2t,1- t,- 2t
(t+ 1) ( )
b(t) = ---1--- 3t- 1,(t- 1)√2t,- t2 - t
(t+ 1)2](homework0121x.png)
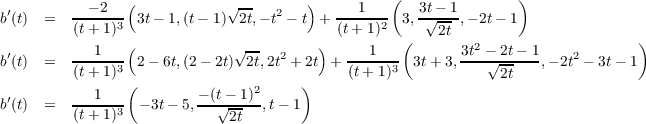
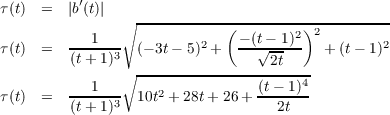
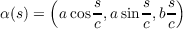
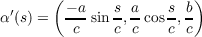

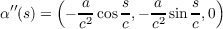

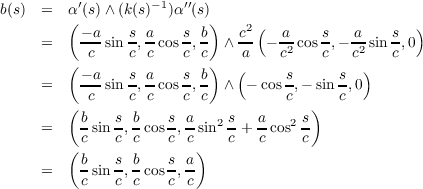

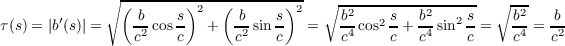

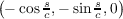 , then the dot product of it and (0,0,1) is zero, implying
that the cosine of the angle between them is zero, which in turn confirms that the angle between them is
, then the dot product of it and (0,0,1) is zero, implying
that the cosine of the angle between them is zero, which in turn confirms that the angle between them is
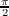 .
.