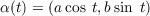
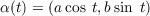
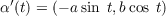
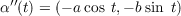
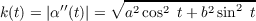
Vertices Using k, we can determine the vertices of α by finding the values of t which make k′(t) zero. Since
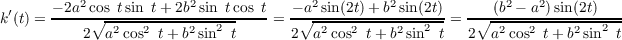
then k′(t) can only be zero when sin(2t) is zero, i.e. at t = 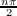 for n ∈ ℤ. Since the domain is t ∈ [0,2π], then there are
vertices at 0,
for n ∈ ℤ. Since the domain is t ∈ [0,2π], then there are
vertices at 0, 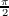 , π,
, π,  , and 2π, however, α(0) = α(2π) so there are only four unqiue vertices at α(0) = (a,0), α(
, and 2π, however, α(0) = α(2π) so there are only four unqiue vertices at α(0) = (a,0), α(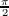 ) = (0,b),
α(π) = (-a,0), and α(
) = (0,b),
α(π) = (-a,0), and α( ) = (0,-b).
) = (0,-b).
With these changes, let’s evaluate the second order Taylor series exansion of α(s), given by
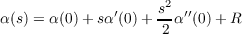 | (2.1) |
where R is the sum of the higher order terms. We know that α(0) is p = (0,0). Because s parametrized α by arc length, then α′(0) is the unit tangent vector at zero, which, since we aligned T with the x-axis, means simply that α′(0) = (1,0). Furthermore, we know α′′(0) = kn to be perpendicular to α′(0), meaning the normal vector n is (0,1), with the sign and magnitude of α′′(0) being determined by k. Substituting these realizations into Equation 2.1, we get
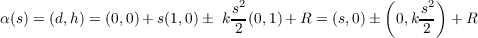
where d and h are as defined in the problem’s statement. Thus denoting R by (Rx,Ry) we have that d = s + Rx and
h = ± k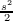 + Ry. The first equation can be rearranged as d-s = Rx, which tells us that s → d as s → 0 since Rx → 0 as
s → 0. The second equation can be rearranged like
+ Ry. The first equation can be rearranged as d-s = Rx, which tells us that s → d as s → 0 since Rx → 0 as
s → 0. The second equation can be rearranged like
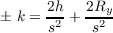
and it informs us that
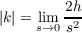
since 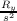 → 0 as s → 0, but because we saw above that s → d as s → 0, then
→ 0 as s → 0, but because we saw above that s → d as s → 0, then
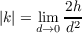
Now, making use of the Fundamental Theorem of The Local Theory of Curves, orient both α and C similarly to the previous problem, i.e. make p be the orgin and align the tangent vector of C at p with the x-axis. With this orientation, for a given d (defined as in the previous problem) hC ≤ hα. Because of this we have
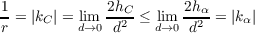
by the previous problem, yielding |kα|≥ 1∕r as needed.
4 do Carmo pg 48 exercise 8 part a
 . Since α is simple and closed, this implies that some circle of radius
. Since α is simple and closed, this implies that some circle of radius  , call it S1, can be situated within and
without intersection with the interior of the trace of α. Hence the area of the interior of α, A, is bounded below by the area
of S1,
, call it S1, can be situated within and
without intersection with the interior of the trace of α. Hence the area of the interior of α, A, is bounded below by the area
of S1, 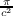 . Thus
. Thus
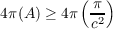
and then making use of the Isoperimetric Inequality we get
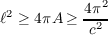
or in other words, ℓ ≥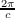 , given the positivity of ℓ and c.
, given the positivity of ℓ and c.