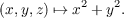
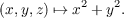
With this definition, f-1(1) is exactly S since S is the set of all points of ℝ which have x2 + y2 = 1. Since the differential df(x0,y0,z0) is the left multiplication by the matrix (2x0,2y0,0), then the only point critical point of the differential is (0,0,0). Putting the previous two ideas together then gives us that 1 is a regular point of the mapping f since f-1(1) = S doesn’t contain the origin of ℝ3. Hence, because f is smooth, then do Carmo’s Proposition 2 of Section 2-2 informs us that S is regular.
Closed Disc The closed disc D is not a regular surface because if it were, then by the definition of a regular surface there would exist a neighborhood V ⊂ ℝ3 of (0,1) ∈D such that D∩V is homeomorphic to some open set of ℝ2, say U. However, the point (0,1) is in D ∩ V but is not an interior point, which contradicts the fact that U, being open in ℝ2, contains only interior points.
Open Disc Setting U ⊂ ℝ2 to the open set {(x,y) ∈ ℝ2 | x2 + y2 < 1} and defining f : U → ℝ by f(u,v) = 0, then D is simply the graph {(u,v,f(u,v)) | (u,v) ∈ U} of ℝ3. So D is a regular surface by do Carmo’s first proposition of chapter two.
Regular Surface Define f : ℝ3 → ℝ by f(x,y,z) = x2 -y2 -z. With this definition, f is smooth and dfp for p = (x0,y0,z0) is the linear map corresponding to the matrix (2x0,-2y0,-1). Since the third parameter of the matrix is -1, then dfp is surjective. Since p was arbitrary, we know the differential to be surjective at all points of ℝ3, and thus all points of ℝ are regular values of the map f. Hence by do Carmo’s second proposition of section 2-2, f-1(0) is a regular surface, but f-1(0) is all points that satify 0 = x2 - y2 - z, which is exactly the set S. So S is regular.
Parametrizations For the following, note that S can equivalently be given by the equation x2 - y2 - z = 0.
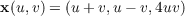
covers S due to the following.
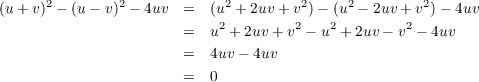
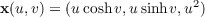
covers S due to the following.
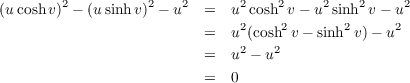
Coverings of the parametrizations ???
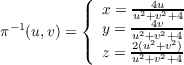
Letting d = u2 + v2 for convience we have the following.
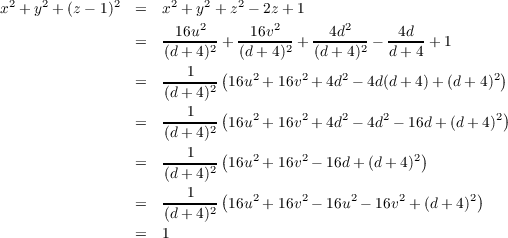
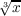 and since both it and the inverse are continuous, then f is a homeomorphism. However, the
inverse is not differentiable at x = 0 since
and since both it and the inverse are continuous, then f is a homeomorphism. However, the
inverse is not differentiable at x = 0 since
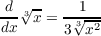
and this is undefined at x = 0.