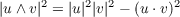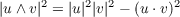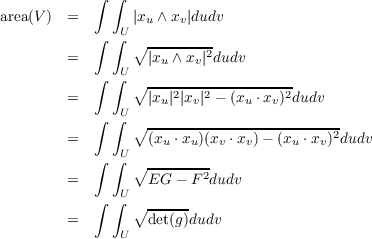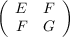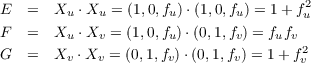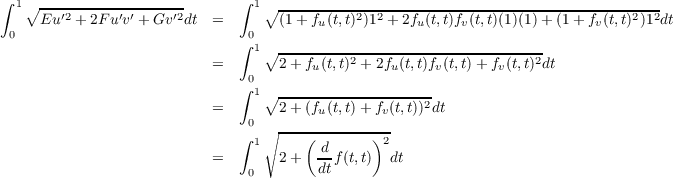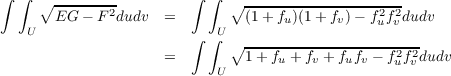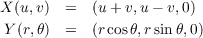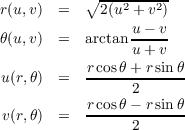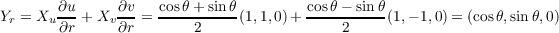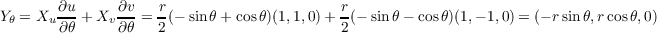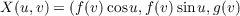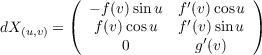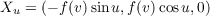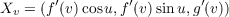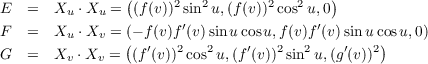Math 501: Differential Geometry

Homework 5
Lawrence Tyler Rush
<me@tylerlogic.com>
March 3, 2013
http://coursework.tylerlogic.com/courses/math501/homework05

1

Using the formula
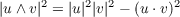
|u∧ v|2 = |u|2|v|2 - (u⋅v)2

we have the following sequence of equations for paramtrization x : U → S for some regular surface S with V = x(U)

∫ ∫ area(V ) = |xu ∧ xv|dudv ∫ ∫U = ∘ |x--∧x-|2dudv ∫ ∫U u v ∘ ---2---2---------2- = U |xu| |xv| - (xu ⋅xv) dudv ∫ ∫ ∘ ------------------------ = (xu ⋅xu)(xv ⋅xv)- (xu ⋅xv)2dudv ∫ ∫U ∘ -------- = EG - F 2dudv ∫ ∫U ------ = ∘ det(g)dudv U
where g = ( E F ) F G

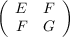
2

Let S be the graph of a smooth function f : ℝ2 → ℝ with coordinate mapping X(u,v) = (u,v,f(u,v)). From this we get that Xu = (1,0,fu) and Xv = (0,1,fv).

(a) Coefficients of The First Fundamental Form

E = Xu ⋅Xu = (1,0,fu)⋅(1,0,fu) = 1+ f2u F = Xu ⋅Xv = (1,0,fu)⋅(0,1,fv) = fufv G = X ⋅X = (0,1,f )⋅(0,1,f ) = 1 + f2 v v v v v

(b) Length of α

Let α(t) be the curve in S with coordinate expression of (t,t) for 0 ≤ t ≤ 1, i.e. α(t) = (u(t),v(t)) where u(t) = t and v(t) = t. With this, the length of α is given by the following.
∫ 1∘ ------------------ ∫ 1∘ ------------------------------------------------ Eu ′2 + 2F u′v′ +Gv ′2dt = (1+ fu(t,t)2)12 + 2fu(t,t)fv(t,t)(1)(1)+ (1+ fv(t,t)2)12dt 0 ∫0 = 1∘2--+f-(t,t)2 +-2f-(t,t)f-(t,t)+-f-(t,t)2dt 0 u u v v ∫ 1∘ -------------------- = 2 +(fu(t,t)+ fv(t,t))2dt ∫0 ∘ ---(--------)- 1 d- 2 = 0 2 + dtf(t,t) dt

(c) Area of V

Let V = X(U) for some bounded open set U of ℝ2. Using the equation we derived in the first problem, we compute the area of V as follows.
∫ ∫ ∘ -------- ∫ ∫ ∘ -------------------- EG - F 2dudv = (1+ fu)(1 + fv) - fu2fv2dudv U ∫ ∫U = ∘1-+-fu +-fv-+-fufv---f2f2dudv U u v

3

Define the following parametrizations of the xy-plane in ℝ3
X(u,v) = (u+ v,u - v,0) Y (r,θ) = (rcosθ,rsin θ,0)
We can then define the change of coordinate function, h : ℝ2 → ℝ2 by
( ∘ ---------------- ) (∘ --------- ) h(u,v) = Y- 1∘X (u,v) = Y -1(u+v, u- v,0) = (u + v)2 + (u- v)2,arctan u---v = 2(u2 + v2),arctan u---v u + v u + v

with inverse

( ) h-1(r,θ) = X -1 ∘Y (r,θ) = X-1(rcosθ,rsin θ,0) = r-cosθ+-rsin-θ, rcosθ--r-sinθ 2 2

resulting in the change-of-coordinate functions at the coordinate level of

r(u,v) = ∘2-(u2 +-v2) u - v θ(u,v) = arctan----- u + v u(r,θ) = rcosθ+-rsinθ- 2 v(r,θ) = rcosθ--rsinθ- 2
Computing Xu = (1,1,0) and Xv = (1,-1,0) we can then compute Y r and Y θ in terms of Xu and Xv as follows
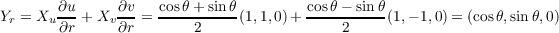
∂u ∂v cosθ +sinθ cosθ- sin θ Yr = Xu ∂r-+Xv ∂r-= -----2----(1,1,0)+ ----2-----(1,- 1,0) = (cos θ,sinθ,0)

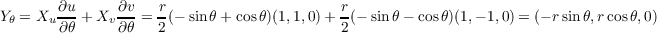
Yθ = Xu ∂u+ Xv ∂v-= r(- sinθ + cosθ)(1,1,0)+ r(- sinθ - cosθ)(1,- 1,0) = (- r sinθ,rcosθ,0) ∂θ ∂θ 2 2

4

The parametrization of the rotation of the regular plane curve, (f(v),g(v), of the xz-plane with x and z coordinates given by f(v) and g(v), respectively, is
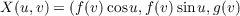
X (u,v) = (f(v)cosu,f(v)sinu,g(v)

(a)

With the above definition of the parametrization, we have the following differential of X.
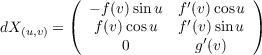
( - f (v)sinu f′(v) cosu ) dX(u,v) = ( f(v) cosu f′(v)sinu ) 0 g′(v)

Since the curve of rotation is a regular curve then g′(v)≠0 for all v which tells us that the columns of dX(u,v) are linearly independent and therefore dX(u,v) is injective.

(b)

With the above definition of the parametrization we get
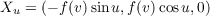
Xu = (- f(v)sinu,f(v)cosu,0)

and

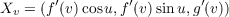
′ ′ ′ Xv = (f(v)cosu,f (v) sinu,g (v))

from which we get

( ) E = Xu ⋅Xu = (f(v))2 sin2u,(f(v))2cos2u,0 F = X ⋅X = (- f (v)f′(v)sinu cos u,f (v)f′(v) sinu cosu,0) u v ( ′ 2 2 ′ 2 2 ′ 2) G = Xv ⋅Xv = (f(v)) cos u,(f (v)) sin u,(g(v))

5 do Carmo Page 109 problem 2

Let φ : S1 → S2 be a local diffeomorphism with S2 orientable. Then there is some N2 : S2 → ℝ3 that is a differentiable field of normal unit vectors. Hence N1 = N2 ∘ φ is differentiable in a neighborhood of any q ∈ S1, but since φ(q) ∈ S2, then N2(φ(q)), which is equal to N1(q), is a unit normal vector. Thus N2 : S1 → ℝ3 is a differentiable field of unit normal vectors, i.e. S1 is orientable.