Math 501: Differential Geometry
Homework 6
Lawrence Tyler Rush
<me@tylerlogic.com>
March 26, 2013
http://coursework.tylerlogic.com/courses/math501/homework06
1
Let S be a compact surface. Because S is in ℝ3, then Heine-Borel tells us that the
surface is bounded. Let v ∈ S2. Because S is bounded, then there exists a plane P with unit-normal v that is
“far enough away” from S that P and S have no intersection. Thus we can bring P in towards S along the
line containing v until it first touches S at some point q. We know that such a point q exists because S is
necessarily closed again due to the implications of Heine-Boral since S is compact. Then P will be tangent
to S with q being the point of tangency. Since v is a unit-normal of P, then N(q) will be v. Hence N is
surjective.
2
Let S be the graph of a smooth function f(x,y).
(a)
Letting x(x,y) = (x,y,f(x,y)) be a coordinate map for S we
have
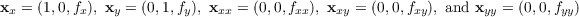
Using the normal given by
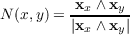
the formula for the normal is
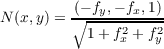
Denoting (1 + fx2 + fy2)-1∕2 by c, we then have
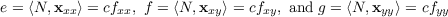
as well as

With these formulas we can use the following formula for the Gauss curvature
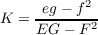
to arrive at
(b)
For f(x,y) = x2 + y2 we have
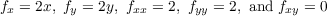
which when using the formula derived in part (a), yields a Gaussian curvature of

which is a nonnegative value that appropaches zero at infinity.
(c)
For f(x,y) = x2 - y2 we have
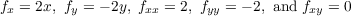
which when using the formula derived in part (a), yields a Gaussian curvature of

which is a nonpositive value that again appropaches zero at infinity.
(d)
For f(x,y) = 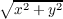 we have
we have

and
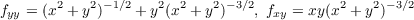
which when using the formula derived in part (a), yields the following Gaussian curvature denoting (x2 + y2)-1∕2 by
c
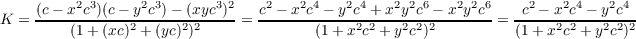
Multiplying the numerator and denominator by c-4 results in a numerator for K of
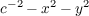
and since c-2 = x2 + y2, then K is identically zero.
(e)
If f is only a function of x, then xx = (1,0,fx), xy = (0,1,0), xxx = (0,0,0),
and xxy = (0,0,0). Due to the latter two, f = ⟨N,xxy⟩ = 0 and g = ⟨N,xxx⟩ = 0, which makes for a zero Gaussian
curvature.
3
Using the following formula for the mean curvature
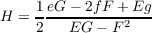
and the formulas for e, f, g, E, F and G from the previous problem to get the following; again we denote (1 + fx2 + fy2)-1
by c
4
Let S1 and S2 be surfaces of the graphs of functions z = f1(x,y) and
z = f2(x,y), respectively, such that both pass through the origin and are tangent to the z = 0 plane. Assume that
f2(x,y) ≥ f1(x,y) ≥ 0. Because zero is a minimum value for both surfaces, then the all partial derivatives f1x, f1y, f2x, f2y
are zero. This then reduces our equations for Gaussian and mean curvature at the origin, derived in problem one,
to

and
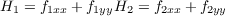
Because f2(x,y) ≥ f1(x,y) ≥ 0 was assumed, then from Calculus we know that
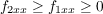
and
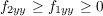
Adding together these two inequalities yields f2xx + f2yy ≥ f1xx + f1yy and multiplying them together yields
f2yyf2xx ≥ f1yyf1xx ≥ 0. At the origin, the former informs us that H2 ≥ H1 and, upon rotating the xy-plane such that
f1xy = f2xy = 0, the latter gives us that K2 ≥ K1.
5
Let S be a compact, orientable surface with inward-pointing normal. Thus
Heine-Borel tells us that the surface is bounded, so we can enclose it within a sphere. Shrink this sphere until it first touches
S and call one of possibly multiple such points p. We know that such points exists since S is closed, again due to
Heine-Borel since S is compact. We can now rotate S and the sphere such that p is identified with the origin, Tp(S) is
identified with the z = 0 plane, and the normal points in the positive direction. Then we can find a neighborhood of p (now
identified with zero) such that S is the graph of some function fS and the sphere is the graph of some function f such that
fS(x,y) ≥ f(x,y) ≥ 0 at the origin. Thus, by the results of the previous problem, the Gaussian curvature of S at p
is greater than or equal to that of a sphere. Thus S has strictly positive curvature since a sphere does as
well.
6
Let S be a minimal surface.
(a)
Because S is a minimal surface, then for the principle curvatures k1 and k2 at
any point p, we have the mean curvature is zero, i.e. 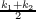 = 0. In other words, k1 = -k2. Hence the Gaussian curvature
k1k2 is simply -k22, implying that it is always nonpositive.
= 0. In other words, k1 = -k2. Hence the Gaussian curvature
k1k2 is simply -k22, implying that it is always nonpositive.
(b)
The results of problem five and the previous part of this problem imply that
there are no compact minimal surfaces in ℝ.
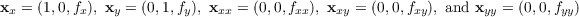
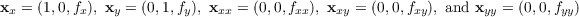
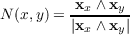
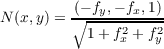


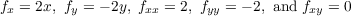

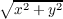 we have
we have

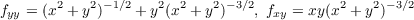
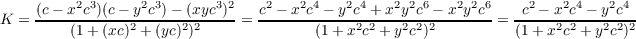
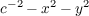
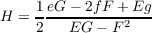


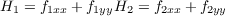
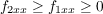
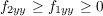
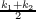 = 0. In other words, k1 = -k2. Hence the Gaussian curvature
k1k2 is simply -k22, implying that it is always nonpositive.
= 0. In other words, k1 = -k2. Hence the Gaussian curvature
k1k2 is simply -k22, implying that it is always nonpositive.