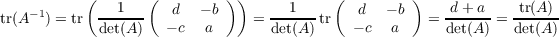Math 501: Differential Geometry
Homework 7
Lawrence Tyler Rush
<me@tylerlogic.com>
April 7, 2013
http://coursework.tylerlogic.com/courses/math501/homework07
1
Taken off the homework.
2
3 do Carmo pg 212 problem 11
Let X be a parametrization of a surface with normal N. Define Y to
be
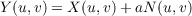 | (3.1) |
for some positive a.
(a)
We know the following to hold where (aij) is the matrix representation of the differential of N. section 3.1 yields and thus combining the two sets of equations above we are left with With this, we can take the cross product of Y u and Y v revealing that Now since K = det([dN]) and H = -1∕2tr([dN]) for Gaussian and mean curvatures of X, then

and
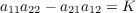
resulting in
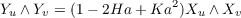
(b)
Let F be the homeomorphism from S to the parallel surface defined by
F(p) = p + aN(p). Thus we have indicating that
![( )
[dFp]{Xu,Xv} = (dFp(Xu ) dFp(Xv )) = (Fu Fv) = ([Fu]X [Fv]X) = 1+ aa11 aa12
aa21 1+ aa22](homework079x.png)
which results in
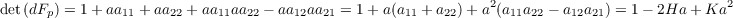 | (3.2) |
Now because of part (a), we know that the normal field for the parallel surface, call it M, at F(p) is the same as the
normal field for S at p, i.e.
 | (3.3) |
We will make use of this to determine the Gaussian and mean curvatures.
Gaussian Curvature
Using the chain rule with subsection 3.3 gives us that
which leads to
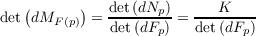 | (3.4) |
The combination of subsection 3.2 and paragraph 3.4 leads to the parallel surface having a Gaussian curvature, K,
of
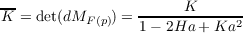
Mean Curvature
Again using the chain rule with subsection 3.3 and employing Lemma A.1 and paragraph 3.4 we find that
Hence the mean curvature, H, is
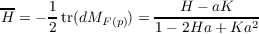
(c)
4 do Carmo pg 229 problem 9
Let S1 and S2 be regular surfaces with a conformal maps φ : S1 → S2 and
ψ : S2 → S3.
(a) Inverses of isometries are isometries
The proof in Problem section 8 part (a) holds for this when λ is the constant
function of 1.
(b) Composition of isometries is an isometry
The proof in Problem section 8 part (b) holds for this when λφ and λψ are
both the constant functions of 1.
5 do Carmo pg 229 problem 10
Let φ : S → S be a rotation about the axis of a surface of revolution,
S. Because it is simply a rotation, φ is the restriction of some linear map of rotation, R : ℝ3 → ℝ3, to S.
Hence for v ∈ S, φ(p) = Ap for some matrix of rotation A. Note that rotational matrices such as A are
orthogonal. Thus we have the following for p ∈ S and v ∈ TpS with some curve α such that α(0) = p and
α′(0) = v

but because A is not dependent on t

resulting in dφp(v) = Av. Thus since A is orthogonal then for any v,w ∈ TpS
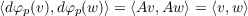
thereby giving us that φ is an isometry.
6
(a)
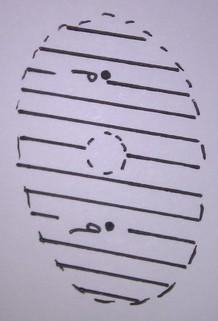
The drawing in Figure 1 has two points p and q in a planar surface for which
there is no curve between them with length equal to the intrinsic distance between the two points. A curve that would
potentially have a length of the intrinsic distance would need to go through the hole in the middle of the surface, but it
obviously cannot while remaining a curve of the surface.
(b)
From our first homework assignment, we know that for any curve α in S with
α(a) = p and α(b) = q, L(α)ab ≥|p-q|. Thus because d(p,q) is the infimum a set of the lengths (from a to b) of curves in S
which pass through p and q at a and b, respectively, then d(p,q) ≥|p - q|.
(c)
7
(a) Coefficients of the first fundamental form.
(b) Relation of M,  , X, and Y
, X, and Y
Since 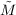 is the map from the domain of X to the domain of Y , then we
have
is the map from the domain of X to the domain of Y , then we
have
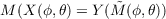 | (7.5) |
for (ϕ,θ) in the domain of X.
(c) Coefficients of the first fundamental form of X
By subsection 7.5 we have
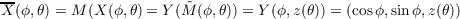
which results in
(d)
In order to have M be a conformal map, we must satisfy and indicating that z′(θ) must be secθ.
(e)
From the result of the previous part of the problem we know
that
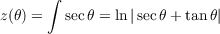
assuming z(0) = 0 and z(θ) > 0 for θ ∈ (0,π∕2).
8
Let S1 and S2 be regular surfaces with a conformal maps φ : S1 → S2 and
ψ : S2 → S3.
(a) Inverses of conformal maps are conformal
Since S1 and S2 are diffeomorphic, then TpS1 = Tφ(p)S2 and dφp = dφφ(p)-1
for p ∈ S2. Thus for vectors v1,v2 ∈ TpS2 = Tφ-1(p)S1, the vectors dφp-1(v1) and dφp-1(v2) are vectors in Tp(S1). So we
have
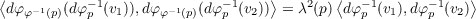
which in turn implies
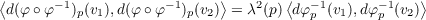
however, φ ∘ φ-1 is the identity map implying that the above equation simplifies to
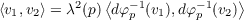
which gives us what we’re looking for
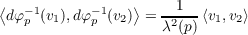
(b) Composition of conformal maps is conformal
Let p ∈ S1 and v1,v2 ∈ TpS. Then we have the following
so for λ(p) = λψ(φ(p))λφ(p) we have
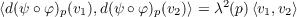
giving us the fact that φ ∘ ψ is conformal since it is a diffeomorphism.
(c)
Appendix
A Helpful Lemmas
Lemma A.1 The trace of the inverse of a two-dimensional matrix A is
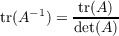
Proof. Let A be the matrix denoted by 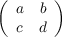 then
then

which in turn leads to
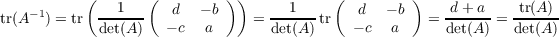
__
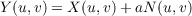
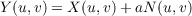

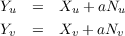
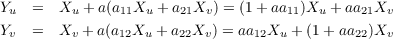
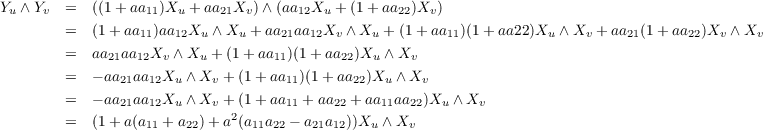

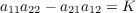
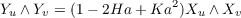
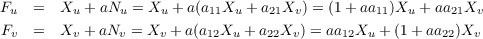
![( )
[dFp]{Xu,Xv} = (dFp(Xu ) dFp(Xv )) = (Fu Fv) = ([Fu]X [Fv]X) = 1+ aa11 aa12
aa21 1+ aa22](homework079x.png)
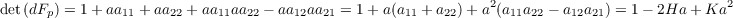

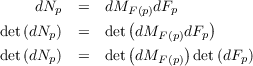
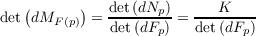
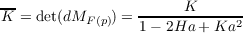
![dN = dM dF
-p1 F-(1p) -p1
dN p = dF p dM F(p)
dFpdN -p1 = dM - 1
- 1 F(p) - 1
tr(dM F(p)) = tr(dFpdNp )
tr(dMF (p)) -1
det(dMF-(p) = tr([dFp]{Xu,Xv}[dNp]{Xu,Xv})
(( ) ( ))
tr(dMF (p)) = det(dMF (p))tr 1 + aa11 aa12 ---1---- a22 - a12
a(a2(1 1 + aa22 det(dN)p() - a21 a11))
det(dNp)----1---- 1 + aa11 aa12 a22 - a12
tr(dMF (p)) = det(dFp) det(dNp) tr aa21 1+ aa22 - a21 a11
1
tr(dMF (p)) = 1--2Ha-+-Ka2-(a22 +aa11a22 - aa12a21 - aa12a21 + a11 + aa11a22)
1
tr(dMF (p)) = 1--2Ha-+-Ka2-((a11 + a22)+ 2a(a11a22 - a12a21))
1
tr(dMF (p)) = 1--2Ha-+-Ka2-(- 2H + 2aK )
tr(dMF (p)) = -- 2(H---aK-)2
1- 2Ha + Ka](homework0715x.png)
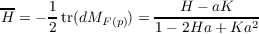


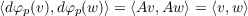
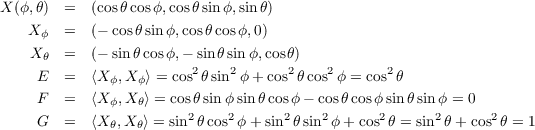
 is the map from the domain of X to the domain of Y , then we
have
is the map from the domain of X to the domain of Y , then we
have
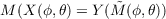
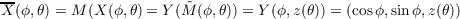
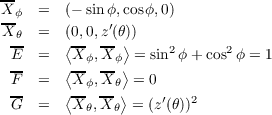

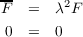
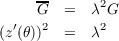
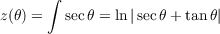
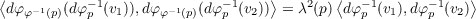
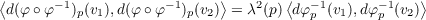
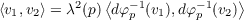
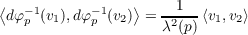

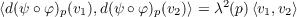
 then
then