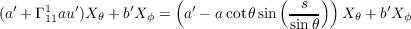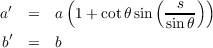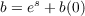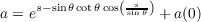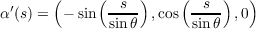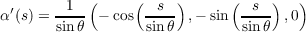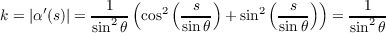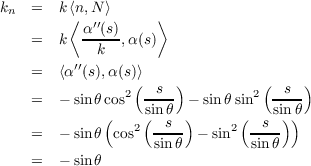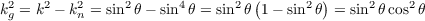Math 501: Differential Geometry
Homework 8
Lawrence Tyler Rush
<me@tylerlogic.com>
April 14, 2013
http://coursework.tylerlogic.com/courses/math501/homework08
1 do Carmo pg 237 problem 1
With F = 0, the Christoffel symbols simplify to
From here, one would use the equation
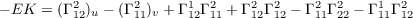
and expand/simplify appropriately to get the desired answer. However, I was not able to find the correct sequence of
expansions/simplifications of the equation resulting from the combination of the above equations.
2 do Carmo pg 237 problem 2
For E = G = λ(u,v) and F = 0 we can use the previous problem to find K to
be
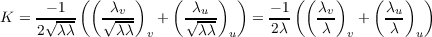
Thus since Δlog λ = 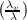 v +
v + 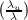 u then we have that
u then we have that
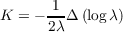
Now let λ = (u2 + v2 + c)-2. To make the following computation easier to follow, we’ll define γ = u2 + v2 + c, i.e.
λ = γ-2. We have the following value of K
With our definition of γ, γu = 4u, γv = 4v, and γuu = γvv = 4. Continuing the equation above we obtain
3
Let S be a surface with geodesic coordinates X so that E = 1 and
F = 0.
(a) Christoffel Symbols
Since E = 1 then Eu = Ev = 0 and thus with F = 0 most of the Christoffel
symbols are zero. Making use of the equations in (2) on pg 232 of do Carmo, we have
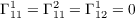
as well as
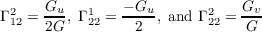
(b) Gaussian Curvature
From the equations of the previous part of the problem, due to most of the
Christoffel Symbols being zero, we have this small equation for the Gaussian curvature.
(c) g for 
Let g = 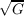 . Then G = g2, Gu = 2ggu and Guu = 2gu2 + 2gguu, so
substituting these equations into the result of the previous part of the problem gets us
. Then G = g2, Gu = 2ggu and Guu = 2gu2 + 2gguu, so
substituting these equations into the result of the previous part of the problem gets us
4
(a)
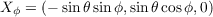
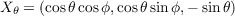
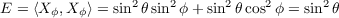
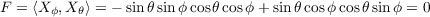
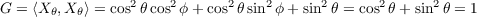
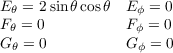
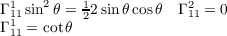
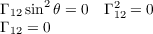
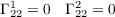
(b)
Let W(s) = a(s)Xθ + b(s)Xϕ. With
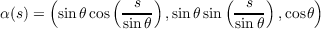
we have u′ = -sin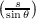 . Thus by equation (1) on page 239 of do Carmo, we have the following since all Christoffel
Symbols are zero except for Γ111
. Thus by equation (1) on page 239 of do Carmo, we have the following since all Christoffel
Symbols are zero except for Γ111
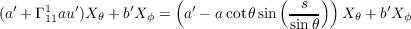
(c)
Solving the ODEs of we find that
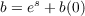
and
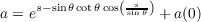
How much does the parallel transport of a vector rotate after one loop?
???
5
With the definition of α above we get
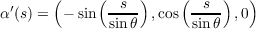
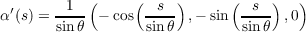
Curvature
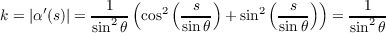
Normal Curvature
Let N be the normal map on the sphere N(p) = p. Than at some p in the trace of α we have
Geodesic Curvature
We have
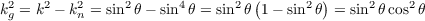
6
(a) Non-length-minimizing positive curvature geodesic
The sketch in Figure 1 has a geodesic between p and q that is not
length minimizing. The curve that travels “the long way” along the great circle containing p and q will be a
geodesic, but not length-minimizing. The geodesic traveling “the short way” will be length-minimizing though.
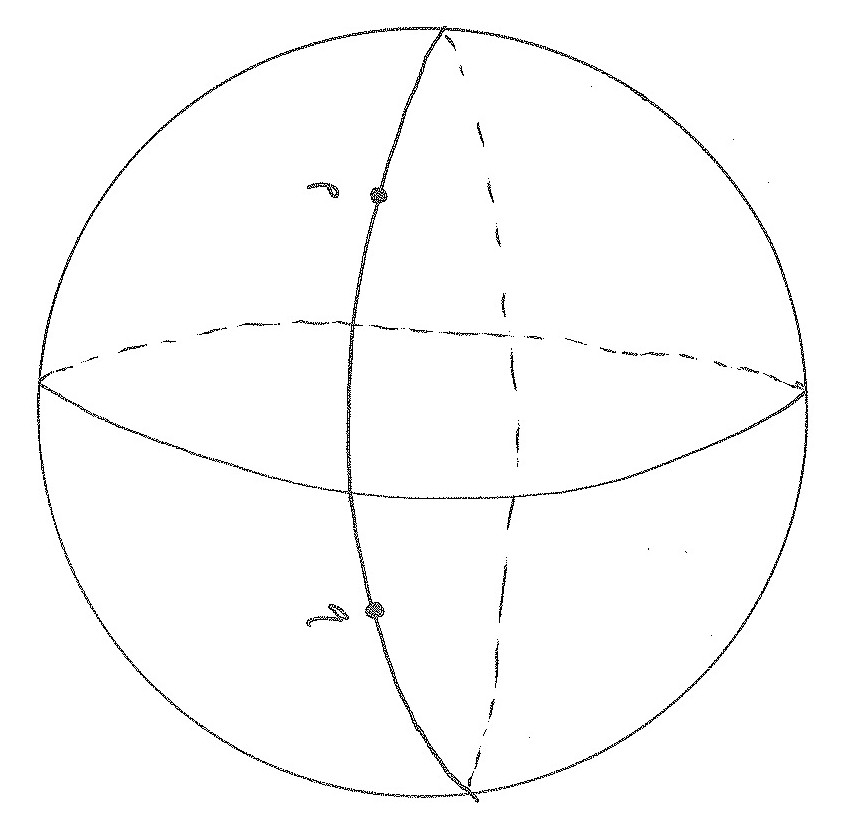
(b) Non-length-minimizing zero curvature geodesic
The sketch in Figure 2 has a geodesic between p and q that is
not length minimizing. Again going the long way, but this time along a horizontal circle of this cylinder.
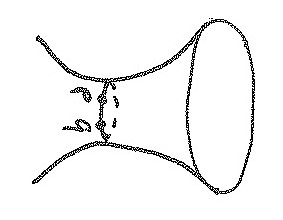
(c) Non-length-minimizing negative curvature geodesic
The sketch in Figure 3 has a geodesic between p and q that is not
length minimizing. Again going the long way, but this time around the “waist” of this surface of revolution.
(d)
(e) A surface where any two points can be joined by a geodesic, but the geodesic is only defined for a
finite amount of time.
The sketch in Figure 4 has a geodesic between every two points, namely the
straight line between them. However, since geodesics need to have constant velocity, then only finite time geodesics could
exist.


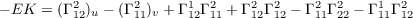
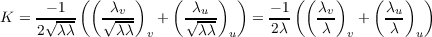
 v +
v + 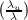 u then we have that
u then we have that
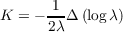
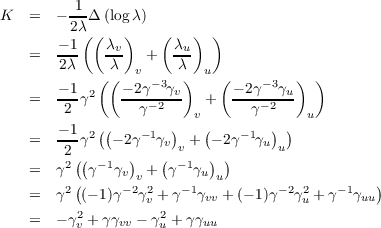
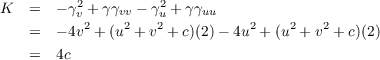
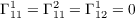
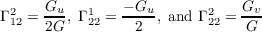
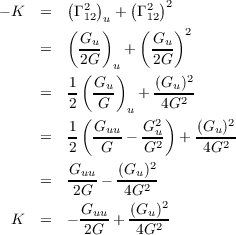
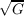 . Then G = g2, Gu = 2ggu and Guu = 2gu2 + 2gguu, so
substituting these equations into the result of the previous part of the problem gets us
. Then G = g2, Gu = 2ggu and Guu = 2gu2 + 2gguu, so
substituting these equations into the result of the previous part of the problem gets us 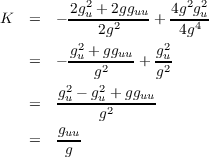
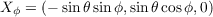
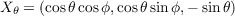
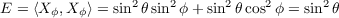
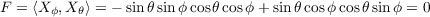
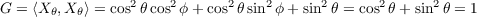
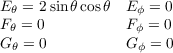
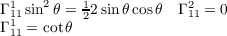
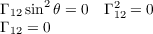
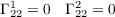
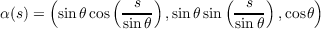
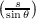 . Thus by equation (1) on page 239 of do Carmo, we have the following since all Christoffel
Symbols are zero except for Γ111
. Thus by equation (1) on page 239 of do Carmo, we have the following since all Christoffel
Symbols are zero except for Γ111