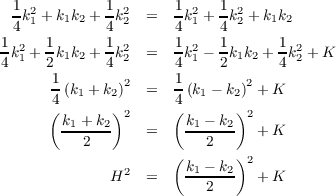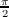 radians.
radians.
Let γ1, γ2, and γ3 be the three piece-wise curves that make up γ. Because each of the peice-wise curves are geodesics,
then their derivative functions are parallel. Hence we have that the vector (1,0,0) will be transported to (0,0,-1) by γ1,
transported from there to (0,0,-1) by γ2, and then transported to (0,1,0) by γ3, returning to the north
pole. Similarly (0,1,0) is transported to (0,1,0) by γ1, then to (-1,0,0) by γ2, and finally to (-1,0,0)
by γ3. Thus the overall transport of (1,0,0) and (0,1,0) along γ is to (0,1,0) and (-1,0,0), respectively.
Since these two elements are a basis, the parallel transport is simply a rotation of the whole space by 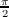 radians.
radians.
Because S is compact, we know from the first problem of homework six that a plane brought in from far enough away until it first touches S, at some p, will be tangent to S. Thus there will be some neighborhood of p for which S will lie entirely on one side of the tangent plane, and because of that fact the curvature at p will be positive. The main point being that S has a point with positive curvature.
Finally, becuase there is a point of S with positive curvature and because its total curvature is zero or negative, then S must also contain a point of negative curvature. Furthermore, because the Gaussian curvature of a surface is continuous, its containing points of positive and negative curvature implies that it must also contain a point of zero curvature.
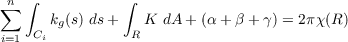
but since the sides of R are geodesics, then each side has zero geodesic curvature. Also, because R is a subset of a sphere, χ(R) = 2 and K = 1. This leaves us with

from Gauss-Bonet theorem. Hence 4π - (α + β + γ) yields the area of R.
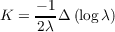
where E = G = λ, which in our case boils down to
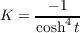
This results in the following total curvature.
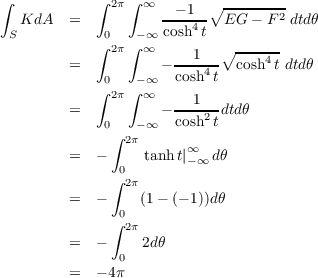
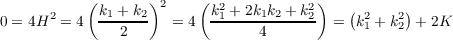
where k1 and k2 are the principle curvatures at a point in S. Hence
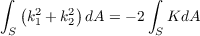
or in other words the total curvature is finite whenever ∫
S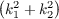 dA is finite, and vice versa.
dA is finite, and vice versa.
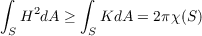
which implies that ∫ SH2dA ≥ 4π, since the Euler characteristic of topological spheres, like S, is 2.
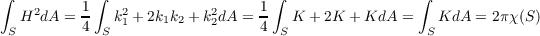
which, for our case of the sphere, means
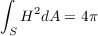
since χ(S) = 2 for S.
Conversely, suppose that the Willmore energy of S is equal to 4π. Since S is a topological sphere, then χ(S) = 2, which implies, by the Gauss-Bonet theorem, that ∫ SKdA = 2πχ(S) = 4π. In other words
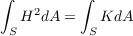
Thus integrating over both sides of A.1, leaves us with
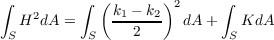
implying that ∫
S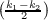 2dA = 0. However
2dA = 0. However 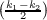 2 is always non-negative, so because it’s integral is zero then it must
be zero. This gives us the equality of the principle curvatures k1 and k2. Hence S must be a round sphere as a round sphere
is the only topological sphere which is also umbilic.
2 is always non-negative, so because it’s integral is zero then it must
be zero. This gives us the equality of the principle curvatures k1 and k2. Hence S must be a round sphere as a round sphere
is the only topological sphere which is also umbilic.
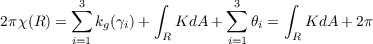 | (6.1) |
where γi are the edges of R.
Now because R is bounded and closed (it contains the edges of the triangle), then it is compact due to Heine-Borel. Thus in light of the second hint in this problem’s statement R must have an Euler characteristic less than or equal to 1, boiling down section 6.1 to ∫ RKdA + 2π ≤ 2π or in other words
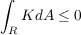
However, because K ≥ 0, then the above integral can never be negative and must be zero, but this in turn implies that K = 0 since K was assumed to be non-negative.
Proof. The result comes from the following sequence of equations.