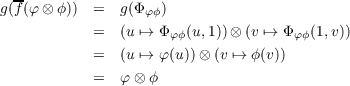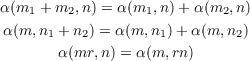
Some Language. Similar to Dummit and Foote [DF04, p. 365], for left R-module N, right R-module M and abelian group L, we will call a map α : M × N → L R-balanced if it satisfies all three of
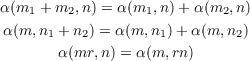

commutes. Furthermore, since α(v,w) = v ⊗ w and β(v,w) = w ⊗ v, then s(v ⊗ w) = w ⊗ v for each v ∈ V and w ∈ W.
Finally, since R is commutative, the above argument symmetrically holds when V and W are swapped as each is a left and right R-module. This implies the existence of a homomorphism s′ : W ⊗RV → V ⊗RW such that s′(w ⊗ v) = v ⊗ w. Hence, s above is invertible and therefore an isomorphism. 1
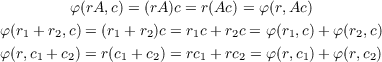
Lemma 2.1. Let ϕ be defined as it is above. For all r ∈ Rn and c ∈ Cn, if ϕ(r ⊗ c) = 0 then r ⊗ c = 0 ∈ Rn ⊗Mn(F)Cn.
Proof. Let the initial conditions of the Lemma’s statement stand. Denote the components of r and c by r1,…,rn and c1,…,cn, respectively. Since ϕ(r ⊗c) = rc = 0 then for each i, ri = 0 or ci = 0. Let i1,…,ik be the indices of the components of r which are zero. Therefore cj = 0 for j ⁄∈{i1,…,ik} Let A ∈ Mn(R) be the matrix with ones along the diagonal, except in rows i1,…,ik which shall be completely zero. Then we have that
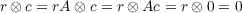
__
Lemma 2.2. For every element x ∈ Rn ⊗Mn(F)Cn there exist elements r ∈ Rn and c ∈ Cn such that x = r ⊗ c.
Proof. As Rn ⊗Mn(F)Cn is made up of finite linear combinations of elements of the form r ⊗ c, it suffices to
only show that any two such elements can be combined into one. So let r1 ⊗ c1 +  + r2 ⊗ c2 be arbitrary in
Rn ⊗Mn(F)Cn. Then by denoting the individual components of r1 by r11,…,r1n and likewise for r2, we can define
A ∈ Mn(F) to be
+ r2 ⊗ c2 be arbitrary in
Rn ⊗Mn(F)Cn. Then by denoting the individual components of r1 by r11,…,r1n and likewise for r2, we can define
A ∈ Mn(F) to be
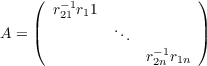
Note that for clarity, we neglect to address the case of a component of r2 being zero, in which case we would set the corresponding diagonal entry in A to zero, and the remainder of the proof holds. Therefore we have
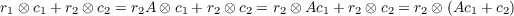
__
Now let r1 ⊗c1 +  + rn ⊗cn in Rn ⊗Mn(F)Cn be such that ϕ(r1 ⊗c1 +
+ rn ⊗cn in Rn ⊗Mn(F)Cn be such that ϕ(r1 ⊗c1 +  + rn ⊗cn) = 0. By Lemma 2.2 there are
r ∈ Rn and c ∈ Cn such that r1 ⊗ c1 +
+ rn ⊗cn) = 0. By Lemma 2.2 there are
r ∈ Rn and c ∈ Cn such that r1 ⊗ c1 +  + rn ⊗ cn = r ⊗ c. By Lemma 2.1 r1 ⊗ c1 +
+ rn ⊗ cn = r ⊗ c. By Lemma 2.1 r1 ⊗ c1 +  + rn ⊗ cn = 0 since
ϕ(r1 ⊗ c1 +
+ rn ⊗ cn = 0 since
ϕ(r1 ⊗ c1 +  + rn ⊗ cn) = ϕ(r ⊗ c) = 0.
+ rn ⊗ cn) = ϕ(r ⊗ c) = 0.
Hence ϕ is an injective linear transformation with a 1-dimensional vector space as a codomain. Then, since ϕ is not the zero map, e.g.
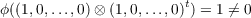
Rn ⊗Mn(F)Cn must also be a one dimensional vector space. Furthermore, in light of Lemma 2.2, ϕ is our explicit isomorphism we need, mapping r ⊗ c to rc.
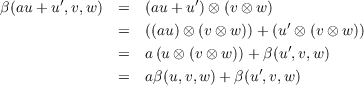
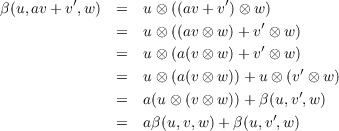
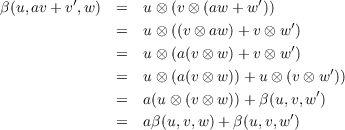
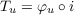 | (3.1) |
where i : V × W → V ⊗ W is the “inclusion” map (v,w) v ⊗ w; i.e. the diagram
v ⊗ w; i.e. the diagram

commutes.
Next, we will use these φu maps to obtain the f for which we’re looking. So define ϕ : U × (V ⊗ W) → X by ϕ(u,v,w) = φu(v ⊗ w). Then equation 3.1 gives us
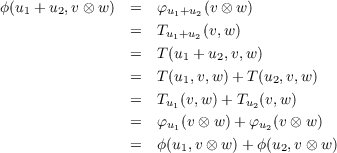
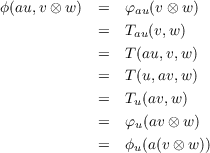
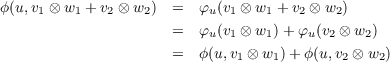
 (u ⊗ (v ⊗ w)). So by defining ψ : U × (V × W) → U × (V ⊗ W) as ψ(u,v,w) = (u,v ⊗ w), we have
ϕ ∘ ψ = f ∘ i′∘ ψ. However, since
(u ⊗ (v ⊗ w)). So by defining ψ : U × (V × W) → U × (V ⊗ W) as ψ(u,v,w) = (u,v ⊗ w), we have
ϕ ∘ ψ = f ∘ i′∘ ψ. However, since
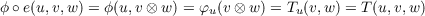
and
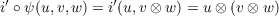
the equation ϕ ∘ ψ = f ∘ i′∘ ψ implies T = f ∘ β.
Given a F-trilinear map T : U × V × W → X where X is some F-vector space, there exists a unique F-linear map f : (U ⊗ V ) ⊗ W → X such that T = f ∘ β
given that we already have the above proof in our hands. So we omit the proof and simply admit the above statement as fact. As there is already grounds for multi-linear universal property of tensor products [Lan02, p. 603], we will overload “the universal property of tensors products” by referring to the above statement, the statement proven in the previous part of this problem, and the original two-dimensional property as “the universal property of tensors products”.
So by part (a) of this problem, we have that β : U ×V ×W → U ⊗ (V ⊗W) is F-trilinear. The same argument holds, by shuffling around parentheses, for β′ : U ×V ×W → (U ⊗V ) ⊗W, implying that it is F-trilinear. Therefore, the universal property of tensor products implies that there exist unique group homomorphisms α′ : (U ⊗V ) ⊗W → U ⊗ (V ⊗W) and α : U ⊗ (V ⊗W) → (U ⊗V ) ⊗W such that α′((u⊗v) ⊗w) = β(u,v,w) and α(u⊗ (v ⊗w)) = β′(u,v,w), i.e. the following diagrams commute

But the uniqueness implies that α′ and α are inverses of each. Thus α is the desired isomophism between U ⊗ (V ⊗W) and (U ⊗ V ) ⊗ W.
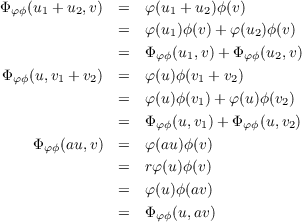
Now define f : U∨× V ∨→ (U ⊗ V )∨ by f(φ,ϕ) = Φφϕ. We yet again have an F-bilinear map here by the following equations, using what we have shown above.
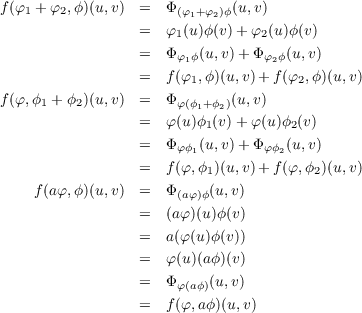
Now we define g : (U ⊗ V )∨→ U∨⊗ V ∨ (this will be our inverse of f) to be the map
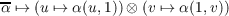
where α : U ×V → F is the map associated with α according to the universal property of tensor products. By the following we see that g is the inverse of f