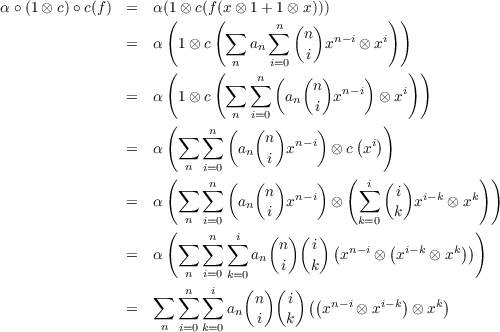Math 503: Abstract Algebra
Homework 2
Lawrence Tyler Rush
<me@tylerlogic.com>
In Collaboration With
Caitlin Beecham
Adam Freilich
Keaton Naff
Matt Weaver
February 6, 2014
http://coursework.tylerlogic.com/courses/upenn/math503/homework02
1
Let R be a commutative ring and G be a finite group.
(a) Show that R ⊗ℤℤ[G] has a structure as a ring
The tensor product R ⊗ℤℤ[G] is already an abelian group, so we need to find a
multiplication operation ⋅ and show that (R ⊗ℤℤ[G],⋅,1R ⊗ 1ℤ[G]) is a monoid as well as the distributive law
holds.
Constructing Multiplication
We first recognize that multiplication in a ring R′ is some associative bilinear operation from R′× R′→ R′. It’s
bilinear because of the distributive law, and associative so that the demands of the aforementioned monoid are
met.
Thus because R and ℤ[G] are both rings, there exist such associative, bilinear maps mR : R × R → R and
mℤ[G] : ℤ[G] × ℤ[G] → ℤ[G]. But then the universal property of tensor products yields mR : R ⊗ℤR → R and
mℤ[G] : ℤ[G] ⊗ℤℤ[G] → ℤ[G] through which mR and mℤ[G] factor, respectively. Thus we can combine these two to form the
linear map mR ⊗mℤ[G] : (R ⊗ℤR) ⊗ℤ(ℤ[G] ⊗ℤℤ[G]) → R ⊗ℤℤ[G]. Because of the commutativity and associativity of the
tensor product, there exists an isomorphism α : (R ⊗ℤℤ[G]) ⊗ (R ⊗ℤℤ[G]) → (R ⊗ℤR) ⊗ℤ(ℤ[G] ⊗ℤℤ[G])
such that α((r ⊗ x) ⊗ (s ⊗ y)) = (r ⊗ s) ⊗ (x ⊗ y) for all r,s ∈ R and x,y ∈ ℤ[G]. Now the composition
mR ⊗mℤ[G] ∘ α : (R ⊗ℤℤ[G]) ⊗ (R ⊗ℤℤ[G]) → R ⊗ℤℤ[G] is a linear map, which, via the universal property of tensor
products, yields a bilinear map m : (R ⊗ℤℤ[G]) × (R ⊗ℤℤ[G]) → R ⊗ℤℤ[G] through which mR ⊗mℤ[G] ∘ α factors. The
map m is our desired multiplication.
Associativity of Multiplication
Because m is bilinear, it satisfies the distributive laws and thus we need only show that m is associative. Also because m
is bilinear, for arbitrary ∑
iri ⊗ xi,∑
jsj ⊗ yj ∈ R ⊗ℤℤ[G]
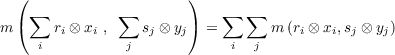
which implies that we need only determine that m(r ⊗x,m(s⊗y,t⊗z)) = m(m(r ⊗x,s⊗y),t⊗z) for all r,s,t ∈ R and
x,y,z ∈ ℤ[G]. So finally, through the use of the associativity of mR and mℤ[G] the following sequence of equations shows m
to be associative. For clarity we set φ = mR ⊗mℤ[G]
Thus R ⊗ℤℤ[G] has a ring structure.
(b) Are R ⊗ℤℤ[G] and R[G] isomorphic?
Because R is a free R-module of rank one, ℤ[G] is a free ℤ-module of rank #G,
and R[G] is a free R-module of rank #G, then we know immediately that R ⊗ℤℤ[G] and R[G] are isomorphic as
R-modules, since their ranks are the same. Furthermore, any homomorphism which takes basis elements to distinct basis
elements will be an R-linear isomorphism. Thus if we can find such an R-module isomorphism and go on to show that it
preserves multiplication between elements of the domain and codomain, then it will also be a ring isomorphism. We
endeavor to find such an isomorphism.
So define α : R × ℤ[G] → R[G] to be the map (r,x) rx. Through use of the properties of R[G], for all r,r1,r2 ∈ R,
x,x1,x2 ∈ R[G], and n ∈ ℤ
rx. Through use of the properties of R[G], for all r,r1,r2 ∈ R,
x,x1,x2 ∈ R[G], and n ∈ ℤ
by which α is ℤ-bilinear. Therefore the universal properties of tensor products yields α : R ⊗ ℤ[G] → R[G] such that
α = α ∘ i where i is the inclusion map. Moreover, α is an isomorphism of modules due to it’s mapping basis elements to
distinct basis elements: α(1 ⊗ [g]) = α(1,[g]) = [g] for each g ∈ G. It remains to be shown that α preserves the operation of
multiplication. The following yields that fact for arbitrary elements ∑
iri ⊗ xi and ∑
jsj ⊗ yj in R ⊗ ℤ[G]
Hence, R ⊗ℤℤ[G] and R[G] are isomorphic rings.
2
Let M and N be two left R-modules over a non-commutative ring
R. Define M ⊙RN to be the quotient of M ⊗ℤN by it’s submodule which is generated by all elements of
the form (r ⋅ m) ⊗ n - m ⊗ (r ⋅ n) where m ∈ M, n ∈ N, and r ∈ R. We will refer to this submodule as
S.
(a)
Define α : M × N → M ⊙RN to be the compositions of the canonical map
i1 : M × N → M ⊗ℤN and the quotient map i2 : M ⊗ℤN → M ⊙RN.
Let Q be an R-module and γ : M × N → Q be a R-bilinear map. Therefore Q is an abelian group and γ is also a
ℤ-bilinear map. Thus the universal property of tensor products gives us the existence of a unique γ′∈ Homgrp(M ⊗ℤN,Q)
such that γ = γ′∘ i1.
Now since S is generated by elements of the form (r ⋅ m) ⊗ n - m ⊗ (r ⋅ n) where m ∈ M, n ∈ N, and r ∈ R and
then S ≤ kerγ′, by which the universal property of quotient modules yields a unique map β ∈ HomR(M ⊙RN,Q) such that
γ′ = β ∘ i2. Hence γ = γ′∘ i2 = β ∘ i2 ∘ i1 = β ∘ α.
Finally, the existence and uniqueness of both γ′ and β, demand that the map β β ∘ α is bijective.
β ∘ α is bijective.
(b) What is M ⊙RN when M, N are R-modules of rank one
Let M and N each be left R-modules of rank 1 with generators m
and n, respectively. Then for the R-module M ⊙RN and for an arbitrary element ∑
imi ⊙ ni ∈ M ⊙RN
while similarly Either one of these implies that M ⊙RN is isomorphic as a R-module to a subring of R, not necessarily proper. However,
combining the two results brings
to light, from which we deduce that
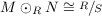
where S is the subring of R generated by elements of the form rs-sr. Note that since R is non-commutative, then S will
not simply be zero.
(c) Give an R such that M ⊙RN is zero for M,N in (b)
Begin with a non-commutative ring, say M2(ℝ), and let M = N = ℝ. Set R
to be the ring generated by elements of the form AB - BA for A,B ∈ M2(ℝ). Then certainly, given the
previous part of this problem, the R-module M ⊙RN will be zero because it will be isomorphic to R ∕ R in this
case.
3
Let G be a finite group with subgroup H. Let F be a field.
(a)
Because F is a field, then the group rings F[G×G] and F[G] are vector spaces
over F with dimension (#G)2 and #G, respectively. Hence F[G] ⊗FF[G] is also a vector space of dimension (#G)2. So
F[G × G] and F[G] ⊗FF[G] are isomorphic. Furthermore, because {[(x,y)]|x,y ∈ G} is a basis for F[G × G] and
{[x] ⊗ [y]|x,y ∈ G} is a basis for F[G] ⊗FF[G], then the map from F[G×G] to F[G] ⊗FF[G] defined by [(x,y)] [x] ⊗ [y]
is an isomorphism, and uniquely so.
[x] ⊗ [y]
is an isomorphism, and uniquely so.
(b)
Again, because F is a field, F[G] and F[G] ⊗FF[G] are vector spaces over F.
Furthermore, because {[x]|x ∈ G} and {[x] ⊗ [y]|x,y ∈ G} are bases for F[G] and F[G] ⊗FF[G], respectively, then defining
α : F[G] → F[G] ⊗FF[G] by [x] [x] ⊗ [x] makes α the unique injective linear homomorphism from F[G] to F[G] ⊗FF[G].
In order for α to be an F-algebra homomorphism, it remains only to prove that α([x][y]) = α([x])α([y]) for all
[x],[y] ∈ F[G]. The following yields that property:
[x] ⊗ [x] makes α the unique injective linear homomorphism from F[G] to F[G] ⊗FF[G].
In order for α to be an F-algebra homomorphism, it remains only to prove that α([x][y]) = α([x])α([y]) for all
[x],[y] ∈ F[G]. The following yields that property:
(c)
Since V and W are left F[G]-modules, then they a free modules each of rank #G.
Since the tensor product of free modules is also a free module, then V ⊗FW is also a left R[G]-module, however, it has rank
(#G)2.
Fix an x ∈ G. Given that ρV (x) ∈ GL(V ) and ρW(x) ∈ GL(W) then we can define ρV ⊗W : G → GL(V ) by
ρV ⊗W(x) = ρV (x) ⊗ ρW(x)
So set A to be the matrix representation of ρV (x) in the basis {[g]|g ∈ G}. Similarly, set B to be the matrix
representation of ρW(x) in the same basis. Also set C to be the matrix representation of ρV ⊗W(x) in the basis
{[g] ⊗ 1|g ∈ G}∪{1 ⊗ [g]|g ∈ G}. Then
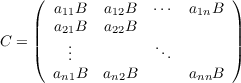
where n = #G and (aij) = A. Therefore we finally arrive at
(d) Extra Credit
4
(a) Show that there is a natural ring isomorphism between ℤ[x,y] and ℤ[x] ⊗ℤℤ[x]
The rings ℤ[x,y] and ℤ[x] ⊗ℤℤ[x] are free ℤ-modules with bases
{xn|n ∈ ℤ≥0}∪{yn|n ∈ ℤ≥0} and {xn ⊗ 1|n ∈ ℤ≥0}∪{1 ⊗ xn|n ∈ ℤ≥0}, respectively. These two bases have the same
cardinality, so any homomorphism that maps the elements of one basis to distinct elements of the other will be a ℤ-module
isomorphism. So once we find such a module isomorphism, we need only show that it preserves the multiplication operation
in order to obtain a ring isomorphism.
Define α : ℤ[x] × ℤ[x] → ℤ[x,y] by  f(x),g(x)
f(x),g(x)
 f(x)g(y). Then for all f,f1,f2,g,g1,g2 ∈ ℤ[x] and n ∈ ℤ we have the
following through heavy use of ring properties of ℤ[x,y].
f(x)g(y). Then for all f,f1,f2,g,g1,g2 ∈ ℤ[x] and n ∈ ℤ we have the
following through heavy use of ring properties of ℤ[x,y].
which implies that α is ℤ-bilinear. Thus the universal property of tensor products gives us α : ℤ[x] ⊗ ℤ[x] → ℤ[x,y] such
that α = α ∘ i where i is the inclusion map. Now α(xn ⊗ 1) = α(xn,1) = xn and α(1 ⊗ xn) = α(1,xn) = yn, making α a
ℤ-module isomorphism. We now only to multiplication to be preserved by α. This is shown by the following for arbitrary
elements ∑
ifi ⊗ gi, ∑
jfj ⊗ gj ∈ ℤ[x] ⊗ℤℤ[x] Hence ℤ[x] ⊗ℤℤ[x] is naturally isomorphic to ℤ[x,y].
(b)
Let c : ℤ[x] → ℤ[x] ⊗ℤℤ[x] be a ring homomorphism such that
c(x) = x⊗ 1 + 1 ⊗x for the polynomial x ∈ ℤ[x]. Therefore, for n ∈ ℤ, c(xn) = (c(x))n. Since {1,x,x2,…} is a basis for ℤ[x],
then c(x) = x ⊗ 1 + 1 ⊗ x completely defines c. Hence, c is unique.
(c)
First note that for n ∈ ℤ we have a formula for c(xn)
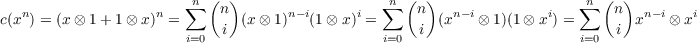
Note that the last line could also be written as ∑
i=0n xi ⊗xn-i. We will make use of both. Then, for any f(x) =∈ ℤ[x],
c(f(x)) = f(x⊗ 1 + 1 ⊗x) = ∑
nan ∑
i=0n
xi ⊗xn-i. We will make use of both. Then, for any f(x) =∈ ℤ[x],
c(f(x)) = f(x⊗ 1 + 1 ⊗x) = ∑
nan ∑
i=0n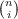 xn-i ⊗xi when f(x) = ∑
nanxn. Given these results, we obtain the following
xn-i ⊗xi when f(x) = ∑
nanxn. Given these results, we obtain the following
???? Seems like there should be a way to manipulate the coefficients above so that (c⊗ 1) ∘c results, but I can’t figure out
how.
(d)
(e)
(f)
(g) Extra Credit
(h) Extra Credit
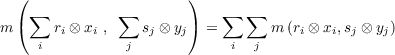
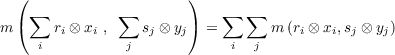
))
= φ∘ α((r ⊗ x)⊗ (mR(s,t)⊗ mℤ[G](y,z)))
= φ((r ⊗ m (s,t))⊗ (x ⊗ m (y,z)))
--- R ----ℤ[G]
= mR(r ⊗mR (s,t))⊗ m ℤ[G ](x⊗ m ℤ[G](y,z))
= mR(r,mR (s,t))⊗ mℤ[G](x,m ℤ[G](y,z))
= mR(mR (r,s),t)⊗ mℤ[G](m ℤ[G](x,y),z)
= m-(m (r,s) ⊗t)⊗ m----(m (x,y)⊗ z)
R R ℤ[G] ℤ[G]
= φ((mR (r,s) ⊗ t)⊗(m ℤ[G](x,y)⊗ z))
= φ∘ α((mR (r,s) ⊗ mℤ[G](x,y))⊗ (t⊗ z))
= φ∘ α((mR-(r⊗ s)⊗ m-ℤ[G](x⊗ y))⊗ (t⊗ z))
= φ∘ α(φ((r ⊗ s) ⊗(x ⊗ y))⊗ (t⊗ z))
= φ∘ α(φ∘ α((r ⊗ x)⊗ (s ⊗ y))⊗ (t⊗ z))
= φ∘ α(m(r⊗ x,s⊗ y)⊗ (t⊗ z))
= m(m (r ⊗ x,s⊗ y),t⊗ z)](homework021x.png)
 rx. Through use of the properties of R[G], for all r,r1,r2 ∈ R,
x,x1,x2 ∈ R[G], and n ∈ ℤ
rx. Through use of the properties of R[G], for all r,r1,r2 ∈ R,
x,x1,x2 ∈ R[G], and n ∈ ℤ 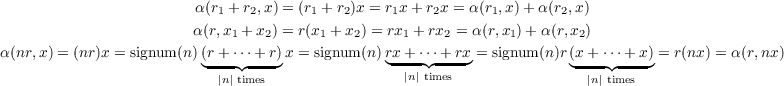
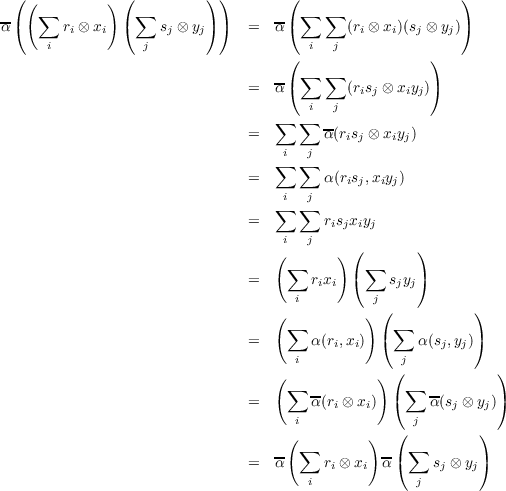
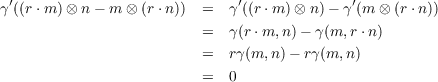
 β ∘ α is bijective.
β ∘ α is bijective.

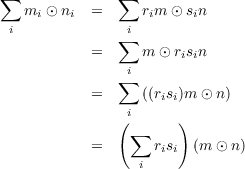
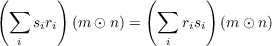
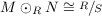
 [x] ⊗ [y]
is an isomorphism, and uniquely so.
[x] ⊗ [y]
is an isomorphism, and uniquely so.
 [x] ⊗ [x] makes α the unique injective linear homomorphism from F[G] to F[G] ⊗FF[G].
In order for α to be an F-algebra homomorphism, it remains only to prove that α([x][y]) = α([x])α([y]) for all
[x],[y] ∈ F[G]. The following yields that property:
[x] ⊗ [x] makes α the unique injective linear homomorphism from F[G] to F[G] ⊗FF[G].
In order for α to be an F-algebra homomorphism, it remains only to prove that α([x][y]) = α([x])α([y]) for all
[x],[y] ∈ F[G]. The following yields that property: ![α ([x][y]) = α([xy])
= [xy]⊗ [xy]
= [x][y]⊗ [x][y]
= ([x]⊗ [x])([y]⊗ [y])
= α([x])α ([y])](homework0213x.png)
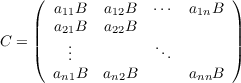
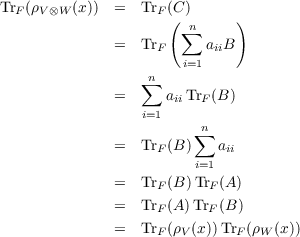
 f(x),g(x)
f(x),g(x)
 f(x)g(y). Then for all f,f1,f2,g,g1,g2 ∈ ℤ[x] and n ∈ ℤ we have the
following through heavy use of ring properties of ℤ[x,y].
f(x)g(y). Then for all f,f1,f2,g,g1,g2 ∈ ℤ[x] and n ∈ ℤ we have the
following through heavy use of ring properties of ℤ[x,y]. 
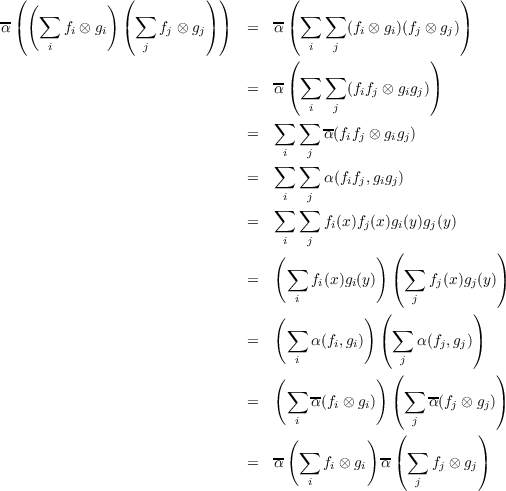
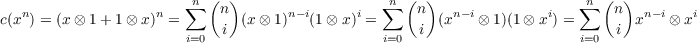
 xi ⊗xn-i. We will make use of both. Then, for any f(x) =∈ ℤ[x],
c(f(x)) = f(x⊗ 1 + 1 ⊗x) = ∑
nan ∑
i=0n
xi ⊗xn-i. We will make use of both. Then, for any f(x) =∈ ℤ[x],
c(f(x)) = f(x⊗ 1 + 1 ⊗x) = ∑
nan ∑
i=0n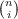 xn-i ⊗xi when f(x) = ∑
nanxn. Given these results, we obtain the following
xn-i ⊗xi when f(x) = ∑
nanxn. Given these results, we obtain the following