Math 503: Abstract Algebra

Homework 3

Lawrence Tyler Rush

<me@tylerlogic.com>

February 15, 2014

http://coursework.tylerlogic.com/courses/upenn/math503/homework03

1

Define D(F) ∈ ℤ[x₁,…,x_n] by

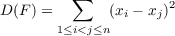
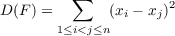D (F) = ∑ (xi - xj)2 1≤i<j≤n

(1.1)

(a)

Existence Given equation 1.1, D(F) can alternatively be specified as

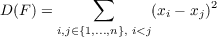
∑ 2 D(F ) = (xi - xj) i,j∈{1,...,n}, i<j

Because any σ ∈ S_n is bijective and because (x_i - x_j)² = ((-1)(x_j - x_i))² = (-1)²(x_j - x_i)² = (x_j - x_i)², then

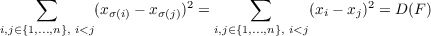
∑ 2 ∑ 2 (xσ(i) - xσ(j)) = (xi - xj) = D(F ) i,j∈{1,...,n}, i<j i,j∈{1,...,n}, i<j

In other words, D(F) is symmetric. Thus there indeed exists a polynomial d ∈ ℤ[x₁,…,x_n] such that d(s₁,…,s_n) = D(F) since every symmetric polynomial in ℤ[x₁,…,x_n] is contained in ℤ[s₁,…,s_n].

Uniqueness There cannot exist two distinct d₁,d₂ ∈ ℤ[x₁,…,x_n] such that d₁(s₁,…,s_n) = d₂(s₁,…,s_n) = D(F) because their existence would contradict the algebraic independence of s₁,…,s_n [Lan02, p. 192] since it would imply d = d₁ - d₂ has d(s₁,…,s_n) = 0.

(b)

Degree n = 2 To find an explicit formula for disc(f) where f(t) is a monic polynomial of degree two, we need to find d(z₁,z₂) ∈ ℤ[z₁,z₂] such that d(s₁,s₂) = (x₁ - x₂)². Because of the existence/uniqueness proven above, we can find such a polynomial and there will be only one. So because s₁ = x₁ + x₂, s₂ = x₁x₂ for n = 2 and because

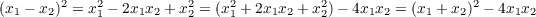
2 2 2 2 2 2 (x1 - x2) = x1 - 2x1x2 + x2 = (x1 + 2x1x2 + x2)- 4x1x2 = (x1 + x2) - 4x1x2

then we can deduce that d(z₁,z₂) = z₁² - 4z₂. Hence for any f(t) = t² + at + b

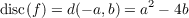
disc(f) = d(- a,b) = a2 - 4b

Degree n = 3 To find an explicit formula for disc(f) where f(t) is a monic polynomial of degree three, we need to find d(z₁,z₂,z₃) ∈ ℤ[z₁,z₂,z₃] such that d(s₁,s₂,s₃) = (x₁ - x₂)²(x₁ - x₃)²(x₂ - x₃)². Again, because of the existence/uniqueness proven above, we can find such a polynomial and there will be only one.

We first notice that d(s₁,s₂,s₃) will be a homogeneous polynomial of degree six in x₁,x₂,x₃. Therefore, since s₁ = x₁ + x₂ + x₃, s₂ = x₁x₂ + x₁x₃ + x₂x₃, and s₃ = x₁x₂x₃,

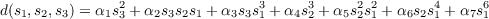
d(s1,s2,s3) = α1s2+ α2s3s2s1 +α3s3s3+ α4s3 + α5s2s2 +α6s2s4+ α7s6 3 1 2 2 1 1 1

for some integers α₁,α₂,α₃,α₄,α₅,α₆,α₇. We will find these values by analyzing the following expansion

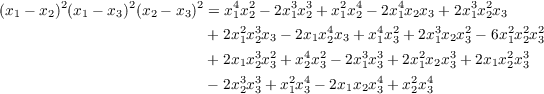(x1 - x2)2(x1 - x3)2(x2 - x3)2 = x41x22 - 2x31x32 + x21x42 - 2x41x2x3 + 2x31x22x3 + 2x21x32x3 - 2x1x42x3 +x41x23 + 2x31x2x23 - 6x21x22x23 3 2 4 2 3 3 2 3 2 3 + 2x1x2x3 + x2x3 - 2x1x 3 + 2x1x2x3 + 2x1x2x3 - 2x32x33 +x21x43 - 2x1x2x43 + x22x43

(1.2)

From this equation, it is immediately apparent that α₆ = α₇ = 0 since s₂s₁⁴ and s₁⁶ would produce monomials containing x₁ raised to a degree higher than 4, but there is no such monomial in the polynomial of equation 1.2. Now, given the expansions

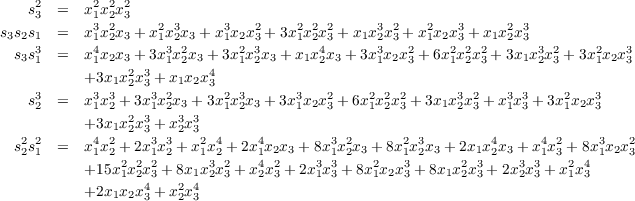
s23 = x21x22x23 s3s2s1 = x31x22x3 + x21x32x3 + x31x2x23 + 3x21x22x23 + x1x32x23 + x21x2x33 + x1x22x33 s s3 = x4x x + 3x3x2x +3x2x3x + x x4x + 3x3x x2+ 6x2x2x2+ 3x x3x2+ 3x2x x3 3 1 1 2 32 3 1 2 3 4 12 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 +3x1x 2x3 + x1x2x3 s32 = x31x32 +3x31x22x3 + 3x21x32x3 + 3x31x2x23 + 6x21x22x23 + 3x1x32x23 + x31x33 + 3x21x2x33 +3x1x22x33 + x32x33 s2s2 = x4x2 +2x3x3 + x2x4+ 2x4x x + 8x3x2x + 8x2x3x + 2x x4x + x4x2 +8x3x x2 2 1 1 2 2 2122 1322 14 22 3 3 13 2 32 13 2 3 2 13 2 33 31 3 2 41 2 3 +15x 1x2x 3 + 8x1x2x3 + x2x3 + 2x1x3 + 8x1x2x3 + 8x1x2x3 +2x2x3 + x1x3 +2x1x2x43 + x22x43

we will strategically evaluate the coefficients of certain monomials in order to give us five linear equations that will allow us to solve for the α variables. So for example, the coefficient in equation 1.2 of x₁²x₂²x₃² is -6, and in the expansions of s₃², s₃s₂s₁, s₃s₁³, s₂³, and s₂²s₁² the coefficients are 1, 3, 6, 6, and 15, respectively. Hence we have the equation

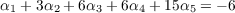
α1 + 3α2 +6α3 + 6α4 + 15α5 = - 6

In the same vein, we evaluate the coefficients for the monomials x₁³x₂²x₃ to get

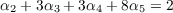
α2 + 3α3 + 3α4 + 8α5 = 2

x₁⁴x₂x₃ to get

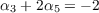
α + 2α = - 2 3 5

x₁³x₃³ to get

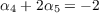
α4 + 2α5 = - 2

and finally x₁⁴x₃² to get

α5 = 1

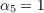
Solving the above five equations we obtain α₁ = -27, α₂ = 18, α₃ = -4, α₄ = -4, and α₅ = 1, which in turn informs us that

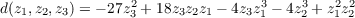
2 3 3 2 2 d(z1,z2,z3) = - 27z3 + 18z3z2z1 - 4z3z1 - 4z2 + z1z2

Hence for any f(t) = t³ + at² + bt + c

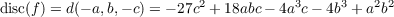
disc(f) = d(- a,b,- c) = - 27c2 + 18abc- 4a3c- 4b3 + a2b2

(c) Extra Credit

2 Newton Polynomials

(a) Find formulas for Newton polynomials p₂, p₃, and p₄ in terms of s₁ through s₄

Since p₂, p₃, and p₄ are symmetric polynomials over ℤ, they can be uniquely represented as a polynomial in terms of the elementary symmetric polynomials over ℤ. Furthermore, they are homogeneous polynomials of degrees 2, 3, and 4, respectively, and must therefore have the forms

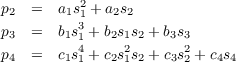
p = a s2+ a s 2 131 22 p3 = b1s1 + b2s1s2 + b3s3 p4 = c1s41 + c2s21s2 + c3s22 + c4s4

for integers a_i, b_i, and c_i.

It’s clear that in order to obtain the appropriate values of p₂, p₃, and p₄, a₁ = b₁ = c₁ = 1 since none of the other clauses in the above equations will be able to account for the x_i², x_i³, and x_i⁴ in each of p₁, p₂, and p₃. Hence, in determining the formula for p_i, our approach will be to start with s₁ⁱ ordered lexicographically and find the coefficient of the leftmost clause that isn’t in p_i and then subtract the product of that coefficient with the appropriate clause on the right hand side of the equations above. We will know which are appropriate by looking at the lexicographical first term of each of the clauses:

Clause	First Term, Lexicographically

s₁²	x₁²
s₂	x₁x₂
s₁³	x₁³
s₁s₂	x₁²x₂
s₃	x₁x₂x₃
s₁⁴	x₁⁴
s₁²s₂	x₁³x₂
s₂²	x₁²x₂²
s₄	x₁x₂x₃x₄

Table 2.1: First terms of elementary symmetric polynomials that generate Newton polynomials.

where these terms have been generated for n = 4.

So for the case of p₂ we start with

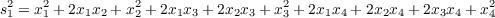
2 2 2 2 2 s1 = x1 + 2x1x2 + x2 +2x1x3 + 2x2x3 + x3 + 2x1x4 + 2x2x4 + 2x3x4 + x4

in which the first term x₁² should remain since it is in p₂, but we need to get rid of the second term 2x₁x₂. Through use of Table 2.1, this implies that a₂ = -2 so that we are left with s₁² - 2s₂ = x₁² + x₂² + x₃² + x₄², and thus the formula for p₂.

For the case of p₃ we start with s₁³ = x₁⁴ + 3x₁²x₂ + ⋅⋅⋅ , leaving off the, currently unimportant, terms after the first two. Again through use of Table 2.1, the coefficient of 3 in the second term informs us that b₂ = -3 so that we are left with s₁³ - 3s₂s₁ = x₁³ + x₂³ - 3x₁x₂x₃ + , which finally informs us that b₃ = 3, leaving us with p₃’s formula: s₁³ - 3s₂s₁ + 3s₂.

Finally, by following the same procedure regarding p₄, we have

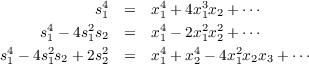
s41 = x41 + 4x31x2 + ⋅⋅⋅ s4- 4s2s = x4- 2x2x2+ ⋅⋅⋅ 4 12 1 22 14 41 2 2 s1 - 4s1s2 + 2s2 = x1 + x2 - 4x 1x2x3 + ⋅⋅⋅

which therefore implies s₁⁴ - 4s₁²s₂ + 2s₂² + 4s₄ = x₁⁴ + x₂⁴ + x₃⁴ + x₄⁴ and yields the formula for p₄.

(b) Extra Credit

(c) Extra Credit

3

Let R be a commutative ring and M be an R-module.

(a) Show the existence of an R-linear “permutation action” of S_n on ⊗_RⁿM

For each σ ∈ S_n, define f_σ : Mⁿ → Mⁿ by (x₁,…,x_n)

(x_σ(1),…,x_σ(n)) for x₁,…,x_n ∈ M. With this definition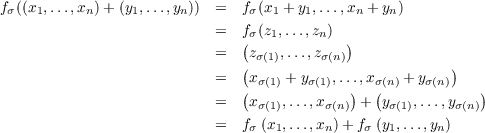

fσ((x1,...,xn )+ (y1,...,yn)) = fσ(x1 + y1,...,xn + yn) = fσ(z1,...,zn) = (z ,...,z ) ( σ(1) σ(n) ) = (xσ(1) +yσ(1),...),xσ((n) + yσ(n) ) = xσ(1),...,xσ(n) + yσ(1),...,yσ(n) = fσ(x1,...,xn) + fσ (y1,...,yn)

for x₁,…,x_n,y₁,…,y_n ∈ M letting z_i = x_i + y_i for each such i. Furthermore,

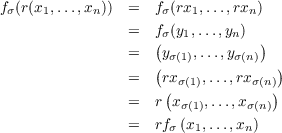
fσ(r(x1,...,xn)) = fσ(rx1,...,rxn) = f(σ(y1,...,yn) ) = (yσ(1),...,yσ(n) ) = rxσ(1),...,rxσ(n) = r(x ,...,x ) σ(1) σ(n) = rfσ(x1,...,xn)

for r ∈ R and x₁,…,x_n ∈ M letting y_i = rx_i for each such i. Therefore each f_σ is an R-multilinear map yielding, via the universal property of tensors, the existence of a unique R-linear homomorphism f_σ : ⊗_RⁿM → Mⁿ through which f_σ factors. Hence f_σ(x₁ ⊗ ⋅⋅⋅

⊗x_n) =

for each σ ∈ S_n and therefore by defining the action of S_n on ⊗_RⁿM by having σ act on x ∈⊗_RⁿM by (i∘f_σ)(x) where i : Mⁿ →⊗_RⁿM is the normal R-multilinear inclusion map, we obtain the desired R-linear permutation action, since i ∘f_σ satisfies the axioms of a group action, being that i and f_σ are each homomorphisms. Note that we omit the use of σ ⋅ x or x ⋅ σ notation in light of the next part of this problem.

(b) Is the action previously defined a left or right action?

Set φ_σ = i ∘f_σ for each σ ∈ S_n so that φ_σ (x1 ⊗ ⋅⋅⋅⊗ xn )

= i∘f_σ

for each x₁,…,x_n ∈ M. For repetitious use later, we point out that φ_τσ = φ_τ ∘ φ_σ for all τ,σ ∈ S_n according to

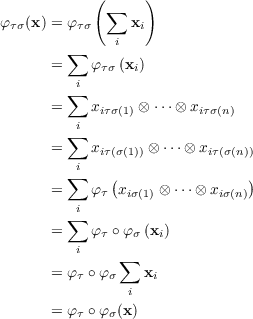( ) ∑ φ τσ(x ) = φτσ xi ∑ i = φτσ(xi) ∑i = xiτσ(1) ⊗ ⋅⋅⋅⊗ xiτσ(n) i = ∑ x ⊗ ⋅⋅⋅⊗ x i iτ(σ(1)) iτ(σ(n)) ∑ ( ) = φτ xiσ(1) ⊗ ⋅⋅⋅⊗ xiσ(n) ∑i = φτ ∘ φσ(xi) i ∑ = φτ ∘ φσ xi i = φτ ∘ φσ(x)

(3.3)

for each x = ∑ _ix_i = ∑ _ix_i1 ⊗ ⋅⋅⋅ ⊗ x_in ∈⊗_RⁿM. With equation 3.3 in hand we see that if we were to attempt to make this action a left action then

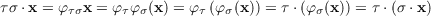
τσ ⋅x = φ x = φ φ (x) = φ (φ (x )) = τ ⋅(φ (x)) = τ ⋅(σ ⋅x) τσ τ σ τ σ σ

and if we were to do so as a right action then

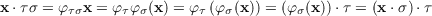
x ⋅τσ = φτσx = φ τφσ(x) = φτ (φ σ(x )) = (φ σ(x))⋅τ = (x⋅σ) ⋅τ

for each x ∈⊗_RⁿM, implying not only that this action is a left action, but that it is not are right action.

(c)

(d) Show R[y₁,…,y_n]S_R^∙(M) for free R-module M with rank(M) = n

Since both R[y₁,…,y_n] is a graded ring where each homogenous component of degree k is the ring of homogenous polynomials of degree k (denote it R^k[y₁,…,y_n]) and S_R^∙(M) is a graded ring where the homogeneous components of degree k is S^k(M), it suffices to prove that R^k[y₁,…,y_n] is isomorphic to S^k(M) for arbitrary k.

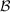Let = {v₁,…,v_n} be a set of free generators on M and Y = {y₁,…,y_n}. We will use ∙ to denote the tensor operation in S^k(M). Define α : M^k → R^k[y₁,…,y_n] and β : Y → S^k(M) by

( ) ∏ ∑n α (m1, ...,mk ) = ( δj(mi)xj) i j=1 β(xi) = vi ∙1∙ ⋅⋅⋅∙ 1

where δ_i ∈ Hom_R-mod(M,R) is the linear operator which takes v_i ∈

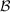to 1 and all other elements of

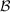to zero. With the product in its definition and because each factor in that product is the sum of linear maps, α is a symmetric k-multilinear map. Therefore, we have that two results:

The existence of an R-module homomorphism α : S^k(M) → R^k[y₁,…,y_n] through which α factors. This comes by way of the universal property of symmetric multilinear maps.
The existence of an R-algebra homomorphism β : R^k[y₁,…,y_n] → S^k(M) through which β factors. This is given by the universal property of polynomial algebras.

Pictorially we have the following commutative diagram.

M k Sk (M ) ααββ- Rk [y ,⋅⋅⋅,y ] Y 1 n

Now, let’s denote x-∙⋅⋅⋅∙x
◟ ◝◜ ◞ _j times ∈ S^k(M) by x^∙j so that x^∙j = x^j ∙ 1∙-⋅⋅⋅∙-1
◟ ◝◜ ◞ _j-1 times since each element of S^k(M) is symmetric. Thus for the generators of S^k(M) and R^k[y₁,,y_n]

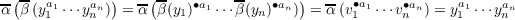
--(-- a1 an ) --(-- ∙a1 -- ∙an) -- ∙a1 ∙an a1 an α β(y1 ⋅⋅⋅yn ) = α β(y1) ⋅⋅⋅β (yn) ) = α(v1 ⋅⋅⋅vn ) = y1 ⋅⋅⋅yn

and

β-(α-(v ∙ ⋅⋅⋅∙ v )) = β-(α(v ,...,v )) = β(x ⋅⋅⋅x ) = v ∙⋅⋅⋅∙v i1 ik i1 ik i1 ik i1 ik

which implies that α and β are inverses of each other. Hence S^k(M) is isomorphic to R^k[y₁, ⋅⋅⋅ ,y_n].

(e) Extra Credit

4

(a) Compute the character of ρ_k

Denote the symmetric and rotational generators of D_2n by s and r, respectively. Since ρ is the homomorphism of the action of D_2n acting on V ₁ = ℝ², then for any arbitrary element sⁱr^j ∈ D_2n, i ∈{0,1}, j ∈{0,…,n - 1}

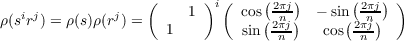
( )i ( (2πj) (2πj) ) ρ(sirj) = ρ(s)ρ(rj) = 1 cos(-n-) - sin(-n) 1 sin 2πnj cos 2πnj

and therefore

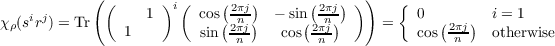
(( )i ( (2πj) (2πj) )) { χρ(sirj) = Tr 1 cos(-n-) - sin( -n) = 0 (2πj) i = 1 1 sin 2πnj cos 2πnj cos -n- otherwise

Hence we can compute the character of ρ_k of any sⁱr^j ∈ D_2n

i j ( i j) ( i j) χρk(s r) = Tr(ρk(s r )⋅⋅⋅χ ρ(s r)) = Tr ρ(sirj)⊗ ⋅⋅⋅⊗ ρ(sirj) ( i j) ( ij ) = T{r ρ(s r ) ⋅⋅⋅Tr ρ(sr ) = 0 ( ) i = 1 cosk 2πjn- otherwise

(b)

(c)

(d) Extra Credit

References

[Lan02] S. Lang. Algebra. Graduate Texts in Mathematics. Springer New York, 2002.