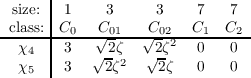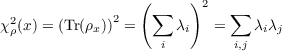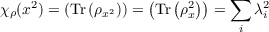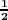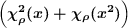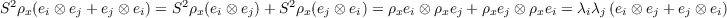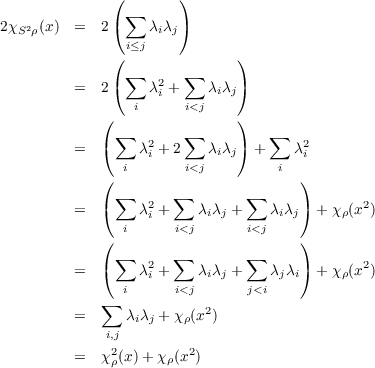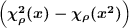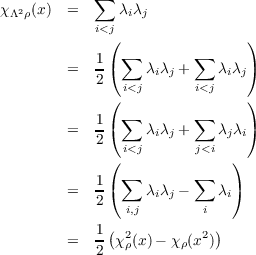Math 503: Abstract Algebra
Homework 5
Lawrence Tyler Rush
<me@tylerlogic.com>
February 27, 2014
http://coursework.tylerlogic.com/courses/upenn/math503/homework05
1
(a) Compute the character table of the Heisenberg group H(F3)
Let a,b,c,x,y,z ∈ F3. Then
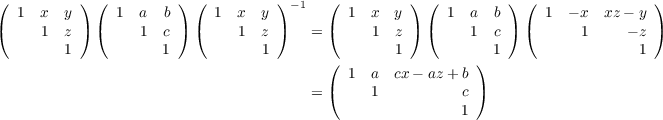
by which we see that
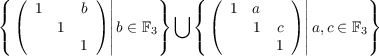
represent the conjugacy classes of H(F3). Thus there are 11 irreducible characters. We will denote the conjugacy classes by
C0, C1, C2, C01, C02, C10, C11, C12, C20, C21, and C22 where
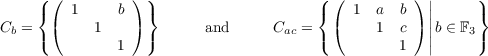
We will denote the eleven characters by χ1 through χ11, with χ1 being the trivial character. With this notation, we have
the following steps of reasoning about the values of the character table.
- The trivial character takes all elements to the identity. So we have:
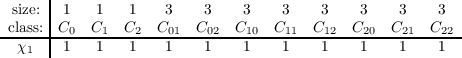
- Since the degrees of the each character must divide the order of the group (which is 27) and the sum of the
squares of the degrees must equal the order of the group, then the degrees of the irreducible characters have
to be 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3 as 9(12) + 2(32) = 27. This gives us the entire first column of the table.
- Define the maps φ : H(F3) → F3 and ϕ : H(F3) → F3 by

Therefore kerφ = 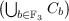 ∪
∪ 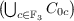 and kerϕ =
and kerϕ = 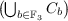 ∪
∪ 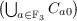 , which implies
H(F3)∕kerφ
, which implies
H(F3)∕kerφ F3 and H(F3)∕kerϕ
F3 and H(F3)∕kerϕ F3. This, in turn, demands that the non-trivial degree-1 characters can
be determined from the non-trivial degree-1 characters on F3. Define χ2 to be the character corresponding to
φ and the character on F3 mapping i
F3. This, in turn, demands that the non-trivial degree-1 characters can
be determined from the non-trivial degree-1 characters on F3. Define χ2 to be the character corresponding to
φ and the character on F3 mapping i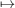 ζi where ζ = e
ζi where ζ = e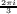 is the third root of unity. Similarly let χ3 be the
character corresponding to ϕ and the character on F3 mapping i
is the third root of unity. Similarly let χ3 be the
character corresponding to ϕ and the character on F3 mapping i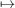 ζi. We thus have:
ζi. We thus have:

- Given that χ2 and χ3 are non-trivial characters of dimension one, their tensor yields another non-trivial
character of dimension one. We can then again tensor the resulting one dimensional character with other
one-dimensional characters to get more one dimensional characters, and then repeat. In this vein we define:
and therefore we are only left with finding the values of χ10 and χ11. This gives us:

- For each conjugacy class which is not one of C0, C1, or C2, the current values of χ1 through χ9, when paired with
themselves and multiplied by the size of the conjugacy class (all have size 3), gives the size of the group. Therefore the
values of χ10 and χ11 must all be zero on these conjugacy classes. We are now left with finding the values of χ10 and
χ11 on C1 and C2.
Now because
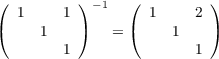
and χ(x) = χ(x-1) for any x ∈ G, then both χ10(x1) = χ10(x2) and χ11(x1) = χ11(x2) for all x1 ∈ C1, x2 ∈ C2.
Furthermore, the orthogonality relations tell us that for x1 ∈ C1 and x2 ∈ C2 (denoting χ10(x1), χ11(x2) by α, β
respectively)
- Pairing the first and second column yields α + β = -3
- Pairing the first and third column yields α + β = -3
- Pairing the second to last row with itself yields αα = 9, i.e. |α| = 3
- Pairing the last row with itself yields ββ = 9, i.e. |β| = 3
By the above constraints, we can see that χ10(x1) = χ11(x2) = 3ζ is a viable solution. This yields
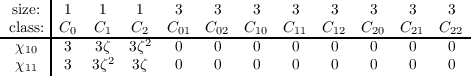
Bringing together all character values from above, we obtain the entire character table, seen in Table 1.1.

Table 1.1: Character table of H(F3)
(b) Extra Credit: Compute the character table of H(Fp) for larger primes
We will compute the character table for H(F5). Put G = H(F5). The conjugacy
classes are similar as in the case of p = 3, there are just more of them. Using the same notation as above, we will denote the
conjugacy classes by
Therefore there are 29 irreducible characters. The degrees of each of these characters must divide |G| = 125, i.e. be 1, 5, 10,
or 25, and the sum of their squares must be 29. The only set of values that satisfy such contraints are 25 1’s and 4 5’s. This
gives us the first column, and of course we have all 1’s in the first row for the trivial representation. Now if we take φ and ϕ
to be as they are defined in the previous subsection, the quotients of G by their respective kernels each result in F5. Thus
each 1-degree character is made up of fifth roots of unity, which we will denote by ζ. Hence we can set χ2 to the character
arising from the character on F5 which takes i ζi, and similarly with χ′ and ϕ. This is similar to our method above.
We can then set the rest of the degree-1 characters to be, i.e. alterating “tensoring” by χ2 and χ3 so that
ζi, and similarly with χ′ and ϕ. This is similar to our method above.
We can then set the rest of the degree-1 characters to be, i.e. alterating “tensoring” by χ2 and χ3 so that
Now the remaining characters will be zero on any classes which are not one of the Ci classes. Furthermore, they will consist
of 5’s on the left and shifts of (ζ,ζ2,ζ3,ζ4). This results in table 1.2.

Table 1.2: Character table of H(F5)
2
(a) Find a non-commutative group G ⊂ S7 with 21 elements.
Since S7 has elements of order 3 and of order 7, e.g. (1 2 3) and
(1 2 3 4 5 6 7), and so has subgroups isomorphic to cyclic groups C3 and C7. We can take a semi-direct product of these
two cyclic groups to obtain the desired group with 21 elements.
Since Aut(C3) is isomorphic to C2, the identity map is the only homomophism in Aut(C3)C7. Hence any C3 ⋊ C7 would
just be isomorphic to the direct product, thereby making G commutative give that the components C3 and C7 are
commutative. Therefore we must find a non-trivial homomorphism φ : C3 → Aut(C7) which will then make
C7 ⋊ φC3 into a semi-direct product. The automorphisms on C7 are defined by their mapping of 1, so define
fn ∈ Aut(C7) by the map m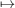 nm for m ∈ C7. Because φ needs to be a homomorphism, we must have
nm for m ∈ C7. Because φ needs to be a homomorphism, we must have
for some yet to be determined fn ∈ Aut(C7). However, notice that no matter what fn is, φ(x) = fnx for
any x ∈ C3. Therefore φ(x)(m) = fnx(m) = nxm, which in turn yields the composition of this semi-direct
product:
 | (2.1) |
For our group we will select n = 2
(b) Determine the conjugacy classes of G
With the fomula from equation 2.1 in hand, the conjugation of (r,y) ∈ C7 ⋊ φC3
by (m,x) is Thus we have the following conjugates when conjugating by (m,x) ∈ C7 ⋊ φC3
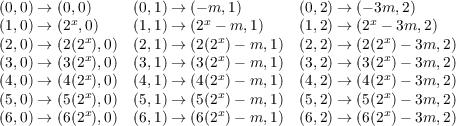
from which we obtain the conjugacy classes:
(c) Compute the character table for G
We will denote the characters by χ1 through χ5 with the first being the character
for the trivial representation. Given this we have the following steps of reasoning about the values of the character
table.
- χ1 is the trivial representation so

- Given the hint in the problem statement, there are three characters of degree 1. Since the degree of the
characters need to divde the order of the group and the squares of their sums need to be 21 (in this case), the
first column of the character table is 1,1,1,3,3
- Define the homomorphism ϕ : G → C3 by ϕ(m,n) = m. Then kerϕ = {(m,0)|n ∈ C7} implying that we can
obtain degree-1 characters from the degree-1 characters of C3. We will assign these to χ2 and χ3 yielding:
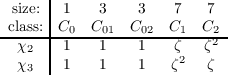
where ζ is the third root of unity, e .
.
- Since 7(1 + ζζ + ζ2ζ2) = 7(3) = 21, then on C1 and C2, χ3 and χ4 both have a value of zero.
- Since (2,0)-1 = (φ(0)(5),0) = (5,0) and because (5,0) ∈ C01 while (2,0) ∈ C02, then the value of χ4 on C01
and C02 must be conjugates of each other. By the same reasoning, the same is true for χ5. If we let α be the
value of χ4 on C01, pairing the fourth row with itself yields αα = 2 and similarly if we let β be the value of
χ5 on C02. Therefore the magnitude of α and β must be
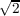 . We quickly realize that α =
. We quickly realize that α = 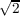 ζ and β =
ζ and β = 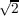 ζ2
is a viable solution, yielding:
ζ2
is a viable solution, yielding:
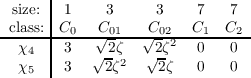
Therefore the whole character table for our G can be seen in table 2.3

Table 2.3: Character table of G = C7 ⋊ φC3
(d) Extra Credit
3 Characters of symmetric and alternating products
Let (V,ρ) be a finite dimensional representation of a finite group G. Let χρ be it’s
character. Fix an x ∈ G. The we can select a basis for V of eigenvectors of ρx, denote it by {ei} and the corresponding
eigenvalues by {λi}. Then
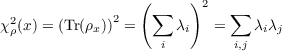 | (3.2) |
and
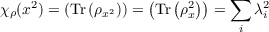 | (3.3) |
(a) Show that the character of (S2(V ),S2ρ) at x ∈ G is 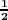
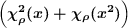
The elements {ei ⊗ ej + ej ⊗ ei}i≤j form a basis for S2(V ). Since
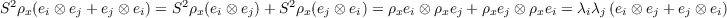
then by equations 3.2 and 3.3
yielding the desired equality.
(b) Show that the character of (Λ2(V ), Λ2ρ) at x ∈ G is 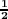
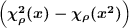
The elements {ei ⊗ ej - ej ⊗ ei}i<j form a basis for Λ2(V ). Since

then by equations 3.2 and 3.3
yielding the desired equality.
(c) Extra Credit
4
(a)
(b)
(c)
(d)
5 Extra Credit
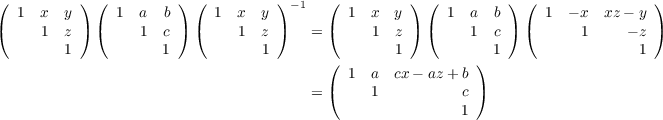
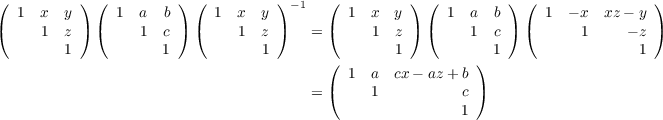
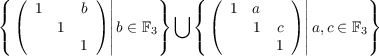
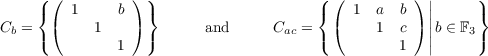
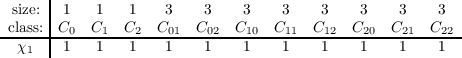

 ∪
∪ 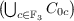 and kerϕ =
and kerϕ = 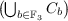 ∪
∪ 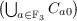 , which implies
H(F3)∕kerφ
, which implies
H(F3)∕kerφ F3 and H(F3)∕kerϕ
F3 and H(F3)∕kerϕ F3. This, in turn, demands that the non-trivial degree-1 characters can
be determined from the non-trivial degree-1 characters on F3. Define χ2 to be the character corresponding to
φ and the character on F3 mapping i
F3. This, in turn, demands that the non-trivial degree-1 characters can
be determined from the non-trivial degree-1 characters on F3. Define χ2 to be the character corresponding to
φ and the character on F3 mapping i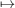 ζi where ζ = e
ζi where ζ = e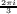 is the third root of unity. Similarly let χ3 be the
character corresponding to ϕ and the character on F3 mapping i
is the third root of unity. Similarly let χ3 be the
character corresponding to ϕ and the character on F3 mapping i ζi. We thus have:
ζi. We thus have:


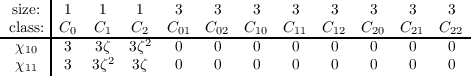
 ζi, and similarly with χ′ and ϕ. This is similar to our method above.
We can then set the rest of the degree-1 characters to be, i.e. alterating “tensoring” by χ2 and χ3 so that
ζi, and similarly with χ′ and ϕ. This is similar to our method above.
We can then set the rest of the degree-1 characters to be, i.e. alterating “tensoring” by χ2 and χ3 so that

 nm for m ∈ C7. Because φ needs to be a homomorphism, we must have
nm for m ∈ C7. Because φ needs to be a homomorphism, we must have

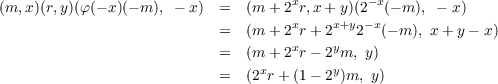
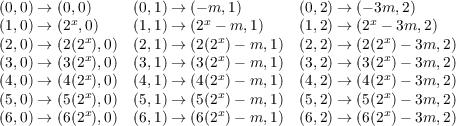


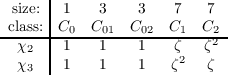
 .
.
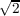 . We quickly realize that α =
. We quickly realize that α = 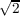 ζ and β =
ζ and β = 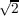 ζ2
is a viable solution, yielding:
ζ2
is a viable solution, yielding: