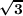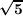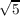+ 
)
- 1), then ℚ(cos(2π∕5)) is simply ℚ(
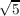), therefore
being an extension of degree two since x2 - 5 is the minimal polynomial of 
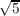. Also since cos(2π∕6) = cos(π∕3) = 1∕2 then
ℚ(cos(2π∕6)) is just ℚ; and hence it is an extension of degree one.
+ )
+ 
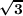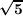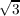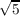∈ ℚ(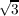
,
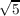) then ℚ(
+ 
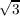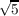) ⊆ ℚ(
,
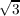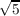). Similarly,
because
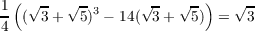
and
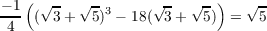
then we also have ℚ(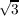
,
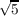) ⊆ ℚ(
+ 
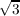). Putting these two results together indicates that ℚ(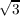
,
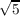) and ℚ(
+ 
)
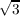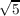are one in the same.
,
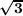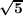) has a finite number of subfields)
,
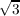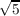) will be a subspace of ℚ(
,
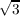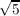) over ℚ. Since
ℚ(
,
) is a finite extension, it is therefore a finite vector space over ℚ, and hence only has a finite number of vector
subspaces. Thus there are only a finite number of subfields, too.
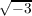), then the non trivial element σ of Aut(K∕Q) is
defined by σ(a + b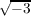
) = a-b
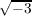for all a + b
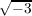∈ K. Since σ* : K[x] → K[x] is defined by σ*(x) = x (where x is the
indeterminate) and σ*|K = σ.
Since f(x) is irreducible over F[x] but reducible as f(x) = g(x)h(x) over K[x] where g(x),h(x) are irreducible in K[x],
then it must be the case that either g(x) or h(x) has some term with a coefficient in K - F, otherwise f(x) would be
reducible in F[x]. Without loss of generality, let g(x) have a term with coefficient in K - F. Since f(x) ∈ F[x], then
σ*(f(x)) = σ*(g(x)h(x)) = (σ*g)(x)(σ*h)(x) = f(x). Because g(x) divides f(x), then it divides (σ*g)(x)(σ*h)(x), but
because g(x) has a term (a + b
)xi for nonzero b ∈ F, then (σ*g)(x) will have the term (a-b
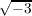)xi and therefore not
be equal to g(x). Hence g(x) = (σ*h)(x).