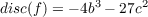
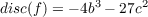
holds for f(T) = T3 + bT + c ∈ F[T] then we can determine the formula for a cubic polynomial g(T) = T3 + AT2 + BT + C ∈ F[T] by substituting S - A∕3 for T [DF04]. So g(S - A∕3) yields a polynomial h(S) so that
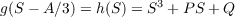
where P = 1∕3(3B - A2) and Q = 1∕27(2A3 - 9AB + 27C). Now if α, β, and γ are roots of h(S), then α - A∕3, β - A∕3, and γ - A∕3 are roots of g(T) since, for instance, g(α - A∕3) = h(α) = 0. Furthermore, since [((α - A∕3) - (β - A∕3))((β - A∕3) - (γ - A∕3))((γ - A∕3) - (α - A∕3))]2 = [(α - β)(β - γ)(γ - α)]2, then the discriminents of g(T) and h(S) are the same, i.e. we can use the formula from the previous part of the problem (again assuming it holds) for the discriminent of h(S). Hence
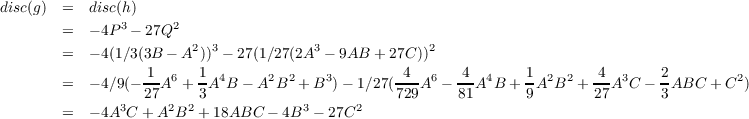
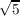 - 1) then 4cos(2π∕5) + 1 =
- 1) then 4cos(2π∕5) + 1 =  , which implies
(4cos(2π∕5) + 1)2 = 16cos2(2π∕5) + 8cos(2π∕5) + 1 is 5. Therefore 16cos2(2π∕5) + 8cos(2π∕5) - 4 is zero. So cos(2π∕5) is
algebraic since it is the root of
, which implies
(4cos(2π∕5) + 1)2 = 16cos2(2π∕5) + 8cos(2π∕5) + 1 is 5. Therefore 16cos2(2π∕5) + 8cos(2π∕5) - 4 is zero. So cos(2π∕5) is
algebraic since it is the root of
![4x2 +2x - 1 ∈ ℚ [x]](homework095x.png) | (3.1) |
since 16x2 + 8x - 4 = 4(4x2 + 2x - 1).
Since sin(2π∕5) = 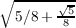 , then 8sin2(2π∕5) - 5 =
, then 8sin2(2π∕5) - 5 = 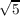 , which implies that 64sin4(2π∕5) - 80sin2(2π∕5) + 25 is 5.
Subtracting five yields 64sin4(2π∕5) - 80sin2(2π∕5) + 20 = 0, and thus that sin(2π∕5) is algebraic since it is the root
of
, which implies that 64sin4(2π∕5) - 80sin2(2π∕5) + 25 is 5.
Subtracting five yields 64sin4(2π∕5) - 80sin2(2π∕5) + 20 = 0, and thus that sin(2π∕5) is algebraic since it is the root
of
![16x4 - 20x2 + 5 ∈ ℚ [x ]](homework098x.png) | (3.2) |
since 64x4 - 80x2 + 20 = 4(16x4 - 20x2 + 5).
 . Thus ℚ(cos(2π∕5))
. Thus ℚ(cos(2π∕5)) ℚ[x] ∕ (4x2 + 2x - 1), implying [ℚ(cos(2π∕5)) : ℚ] = 2.
ℚ[x] ∕ (4x2 + 2x - 1), implying [ℚ(cos(2π∕5)) : ℚ] = 2.
The polynomial, 16x4 - 20x2 + 5, from equation 3.2 is irreducible over ℚ since it meets Eisenstein’s criteria, that is
5 ⁄|16, 5|20, 5|5, and 52 ⁄|5. So ℚ(sin(2π∕5)) ℚ[x] ∕ (16x4 - 20x2 + 5), and therefore [ℚ(sin(2π∕5)) : ℚ] = 4.
ℚ[x] ∕ (16x4 - 20x2 + 5), and therefore [ℚ(sin(2π∕5)) : ℚ] = 4.
Does one contain the other?
Since sin(2π∕5) = 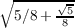 , then
, then
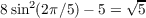 | (3.3) |
Therefore, because cos(2π∕5) = 1∕4(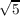 - 1) we have
- 1) we have
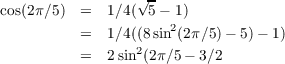
 ℚ[x] ∕ (4x2 + 2x - 1) contains both the
roots ±cos(2π∕5) of 4x2 + 2x - 1 then the field is Galois, as it is simply the splitting field of the separable
polynomial 4x2 + 2x - 1. Since the field is an extension of degree two over ℚ, then it’s Galois group is simply
ℤ ∕2 ℤ.
ℚ[x] ∕ (4x2 + 2x - 1) contains both the
roots ±cos(2π∕5) of 4x2 + 2x - 1 then the field is Galois, as it is simply the splitting field of the separable
polynomial 4x2 + 2x - 1. Since the field is an extension of degree two over ℚ, then it’s Galois group is simply
ℤ ∕2 ℤ.
Galois group of ℚ(sin(2π∕5))
Now attempting to determine the Galois group for ℚ(sin(2π∕5)) ℚ[x] ∕ (16x4 - 20x2 + 5) is slightly more tricky. Certainly
the roots ±sin(2π∕5) = ±
ℚ[x] ∕ (16x4 - 20x2 + 5) is slightly more tricky. Certainly
the roots ±sin(2π∕5) = ±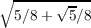 of 16x4 - 20x2 + 5 are contained within, but it is not immediately clear whether or
not the roots ±
of 16x4 - 20x2 + 5 are contained within, but it is not immediately clear whether or
not the roots ±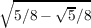 are contained in the field. We note that
are contained in the field. We note that
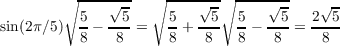
which implies that
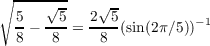
Equation 3.3 informs us that 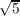 is in ℚ(sin(2π∕5)), and being a field, (sin(2π∕5))-1 is in definitely in ℚ(sin(2π∕5)); hence
is in ℚ(sin(2π∕5)), and being a field, (sin(2π∕5))-1 is in definitely in ℚ(sin(2π∕5)); hence
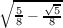 (and its negation) is also in the field. Hence all the roots of 16x4 - 20x2 + 5 are contained within the field. Thus
the field is therefore a splitting field of a separable polynomial, and hence Galois.
(and its negation) is also in the field. Hence all the roots of 16x4 - 20x2 + 5 are contained within the field. Thus
the field is therefore a splitting field of a separable polynomial, and hence Galois.
Now since ℚ(sin(2π∕5)) has degree four over ℚ, then its Galois group has size four. Automorphisms of the Galois group
will just permute the roots ±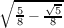 , ±
, ± , because of which we can completely define two non-trivial
automorphisms by
, because of which we can completely define two non-trivial
automorphisms by
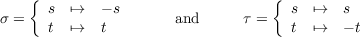
letting s = 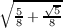 and t =
and t = 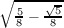 . From this we see that σ2 and τ2 are both the identity automorphism and that the
the third non-trivial automorphism is
. From this we see that σ2 and τ2 are both the identity automorphism and that the
the third non-trivial automorphism is
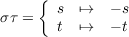
also with (στ)2 being the identity automorphism. Hence Gal(ℚ(sin(2π∕5))∕ ℚ) = {1,σ,τ,στ}, but futhermore, since each non-trivial element has order two, then Gal(ℚ(sin(2π∕5))∕ ℚ) must be the Klein-four group.
[DF04] D.S. Dummit and R.M. Foote. Abstract Algebra. John Wiley & Sons Canada, Limited, 2004.
[Wol14a] Wolfram—Alpha. http://www.wolframalpha.com/input/?i=cos(2*pi/5), April 2014.
[Wol14b] Wolfram—Alpha. http://www.wolframalpha.com/input/?i=sin(2*pi/5), April 2014.