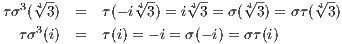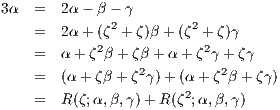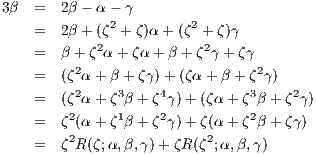then the roots are ±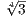 ,±i
,±i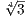 . So the splitting field of T4 - 3 over ℚ is ℚ(
. So the splitting field of T4 - 3 over ℚ is ℚ(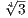 ,i
,i ). This yields
). This yields
 | (1.1) |
as the possible elements of the Galois group of K, leaving us with a potential Galois group of size 8.
Now since T4 - 3 is irreducible over ℚ (by Eisenstein’s criteria), then ℚ( ) is an extension of degree four. In ℚ(
) is an extension of degree four. In ℚ(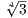 ),
T4 - 3 factors as T4 - 3 = (T -
),
T4 - 3 factors as T4 - 3 = (T -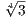 )(T +
)(T + 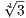 )(T2 +
)(T2 + 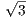 ) where (T2 +
) where (T2 + 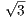 ) is irreducible with roots ±i
) is irreducible with roots ±i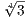 . Then
K = ℚ(
. Then
K = ℚ(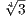 ,i
,i ) is an extension of degree two over ℚ(
) is an extension of degree two over ℚ(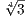 ). Therefore K has degree 8 over ℚ, and this implies
that the 8 automorphisms above are all elements of the Galois group of K, and furthermore are the only
elements.
). Therefore K has degree 8 over ℚ, and this implies
that the 8 automorphisms above are all elements of the Galois group of K, and furthermore are the only
elements.
Note that every automorphism σ of the Galois group of K will take 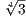 to an element in K of the form (-1)min
to an element in K of the form (-1)min and
therefore take i
and
therefore take i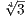 to an element of the form (-1)rin+1
to an element of the form (-1)rin+1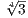 for m,n,r ∈{0,1}. This then defines the mapping of i
as
for m,n,r ∈{0,1}. This then defines the mapping of i
as
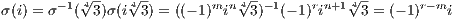
Conversly if we were to define the the mapping of only 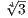 and i, mapping them to (-1)min
and i, mapping them to (-1)min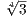 and (-1)ri, respectively,
we can recover where i
and (-1)ri, respectively,
we can recover where i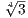 is mapped to as (-1)ri(-1)min
is mapped to as (-1)ri(-1)min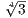 = (-1)r+min+1
= (-1)r+min+1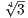 , resulting in one of the automorphisms in
equation 1.1. Hence, we can simply define an automorphism in Gal(K∕ ℚ) by its mapping of
, resulting in one of the automorphisms in
equation 1.1. Hence, we can simply define an automorphism in Gal(K∕ ℚ) by its mapping of 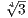 to any other root of T4 - 3
and its mapping of i to ±i.
to any other root of T4 - 3
and its mapping of i to ±i.
So let’s define

form which we see |σ| = 4 and |τ| = 2. Furthermore we see that σ and τ generate Gal(K∕ ℚ) since any automorphism
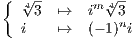
in the Galois group, where m ∈{0,1,2,3} and n ∈{0,1} is equal to σmτn. Finally we have