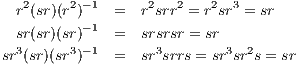
In the last homework we saw that the splitting field of T4 - 3 over ℚ is finite Galois with Galois group D8. In the group D8 we have subgroups ⟨sr⟩≤⟨sr,r2⟩≤ D8 where s is the mirror symmetry and r is the rotational symmetry.
The fact that r(sr)r3 = rsr4 = rs = sr3 demonstrates that ⟨sr⟩ is not normal in D8. Since ⟨sr,r2⟩ = {1,r2,sr,sr3}, then
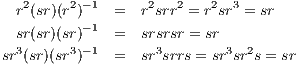
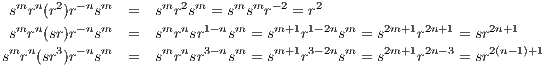
Thus for F = ℚ, K = Ω⟨sr,r2⟩
and L = Ω⟨sr⟩ where Ω = ℚ(
,i) is the splitting field of T4 - 3 over ℚ, we will have our
desired scenario.
We can determine the fixed fields K and L as follows. Define s and r as the automorphisms
where θ =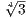 
. This then sets
Because ⟨sr⟩ is a subgroup of size two, then L∕ ℚ must be an extension of degree four. Since
and ℚ(θ(i- 1)) ⊂ Ω is an extension of degree four, then we must have L = ℚ(θ(i- 1)). Similarly, ⟨sr,r2⟩ is a subgroup of size four, and ℚ(iθ2) ⊂ ℚ(θ(i - 1)) ⊂ Ω has degree two. Then since
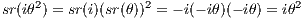
and
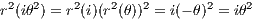
then we have K = ℚ(iθ2).
Proof. If K is a non-trivial finite extension of ℝ, then it is algebraic over ℝ. For any α ∈ K - ℝ, it’s minimal polynomial mα(x) ∈ ℝ[x] is nonlinear, irreducible. Since all odd degree polynomials in ℝ[x] have a real root, we conclude deg(mα(x)) is even. However, [K : ℝ] = deg(α) = deg(mα(x)) and thus K has even degree. __
By the preceeding lemma, [L : ℝ] is even. Then so is the size of Gal(L∕ ℝ). So define H to be a 2-Sylow subgroup of Gal(L∕ ℝ). Then the index of H in Gal(L∕ ℝ) is not divisible by two and therefore E = LH is an extension of ℝ with odd degree. However, according to Lemma 3.1, the only such extension is ℝ itself. Thus E = ℝ. This furthermore implies that H = Gal(L∕ ℝ), which, since H is a 2-Sylow subgroup, also means Gal(L∕ ℝ) is a 2-group.
Proof. Any quadratic over ℂ has roots in ℂ provided by the quadratic formula. __
Let f(T) ∈ ℂ[T] and α be a root of f(T). Assume by way of contradiction that ℂ(α) is a nontrivial extension over ℂ. Then ℂ(α) is an extension of ℝ of even degree by Lemma 3.1. Thus, Gal(ℂ(α)∕ ℝ) would be a nontrivial 2-group with size greater than or equal to 4, by part (a) of this problem. But then Gal(ℂ(α)∕ ℝ) would have a subgroup of size 4 (Theorem 6.1 [DF04]: “p-groups have subgroups of all applicable sizes”), i.e. there would exist an extension K∕ ℂ with degree 2. However, this contradicts the Lemma 3.2, and hence ℂ(α) is trivial, implying α ∈ ℂ.