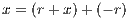
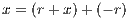
would imply x is rational by the closure of addition in the field of rationals; but since x is assumed to be irrational, so must be r + x.
Similarly, rx must be irrational since
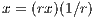
and the field of rationals is closed under multiplication.
Proof. Assume for later contradiction that 3 is rational. Then we can find integers m,n which are not both even
such that m∕n = 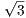 . Therefore
. Therefore
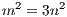
This equation then demands that if n2 is even, then so must be m2 (and therefore m), and similarly if n2 is odd, then so must be m2 (and therefore m). Because m and n were assumed to not both be even, then m and n must both be odd. Thus we can set m = 2p + 1 and n = 2q + 1. Furthermore the above equation implies that
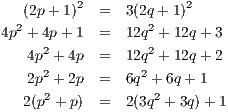
Since 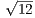 = 2
= 2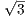 the previous problem and the above lemma together imply that
the previous problem and the above lemma together imply that  is irrational.
is irrational.
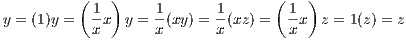
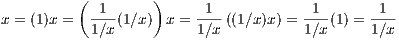
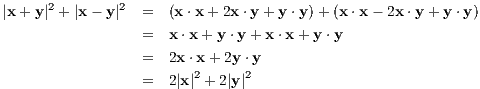
Geometrically, if |x| and |y| are the two lengths of two adjacent sides of a parallelogram, then |x + y| and |x-y| would be the lengths of the two diagonals. So this equation reveals that the sum of the squares of the diagonals of a parallelogram is equal to twice the sum of the squares of its sides.
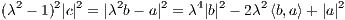 | (5.1) |
Now assuming that |x - a| = λ|x - b| for some point x ∈ ℝk we get the following sequence of equations.
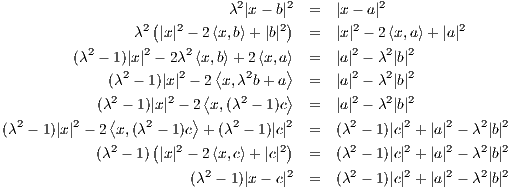
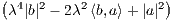 , so making that
substitution into the last line from the sequence of equations above, we continue:
, so making that
substitution into the last line from the sequence of equations above, we continue: 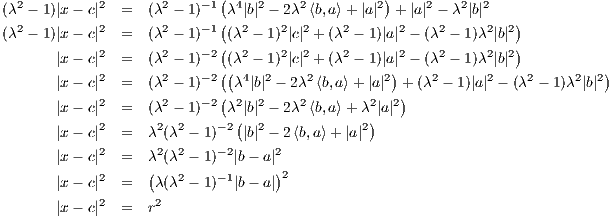
What happens when λ = 1? When λ = 1, we’d be interested in all points x ∈ ℝk where |x-a| = |x-b|. However the points that satisfy this are the points in the hyper-plane that perpendicularly bisects the line segment, which of course has no notion of a radius since it is a hyper-plane and not a hyper-sphere. Hence it makes no sense to inquire about a sphere of radius r = λ(λ2 - 1)-1|b - a|; this is dually supported by the denominater, (λ2 - 1), having a value of zero when λ = 1. In a silly way of thinking, it’s as if the sphere gets so big (as λ approaches 1) that it “becomes a plane”.
Proof. First note that if any Si is the empty set it can simply be neglected. So fix an ordering of each of the elements of each set Si and label them as follows

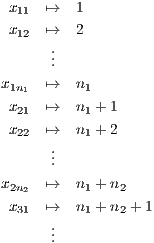
Let S1,S2,S3,… each be a finite set. The problem here is that these sets are not mutually disjoint, but nevertheless, we can define the sets T1,T2,T3,… as T1 = S1 and Tn = Sn -∩j=1n-1Sj and furthermore, ∩j=1n-1Tj = ∩j=1n-1Sj. So due to the above lemma, ∩j=1n-1Tj is countable and therefore so is A = ∩j=1n-1Sj.
![Sn = {z ∈ ℂ | ∃ a0,...,an ∈ ℤ ∩ [- n,n] ∋ anzn + an-1zn-1 + ⋅⋅⋅+a1z + a0 = 0}](homework0117x.png)
Now with this definition, the set A = ∪i=1∞Si will contain only algebraic numbers, but it will furthermore contain all of
the algebraic numbers since if z is the root of anxn +  + a1x + a0 and some ai has |ai| > n, then z will be in the SN
where N = max(|a0|,…,|an|) since z will also be a root of 0xN + 0xN-1 +
+ a1x + a0 and some ai has |ai| > n, then z will be in the SN
where N = max(|a0|,…,|an|) since z will also be a root of 0xN + 0xN-1 +  + 0xn+1 + anxn +
+ 0xn+1 + anxn +  + a1x + a0. Also,
because a polynomial of degree n has at most n roots and the set ℤ ∩ [-n,n] is finite for any n, then each of the sets Si
are finite. Therefore, the previous problem gives us that A (the set of algebraic numbers) is a countable
set.
+ a1x + a0. Also,
because a polynomial of degree n has at most n roots and the set ℤ ∩ [-n,n] is finite for any n, then each of the sets Si
are finite. Therefore, the previous problem gives us that A (the set of algebraic numbers) is a countable
set.
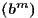 1∕n =
1∕n = 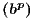 1∕q
1∕q
So it makes sense to define br = 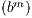 1∕n
1∕n
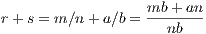
which in turn allows
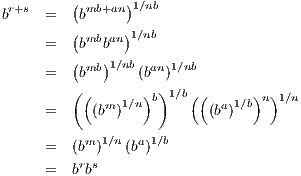
Each rational number r = p∕q with p,q ∈ ℤ, q≠0, is the root of f(z) = qz -p, implying that the rational numbers are a subset of the countable algebraic numbers, i.e. they’re countable. So because the rational numbers are countable, the union of the rational and irrational numbers are the reals, and the reals are uncountable, then the irrational numbers are necessarily uncountable.