Math 508: Advanced Analysis
Homework 2
Lawrence Tyler Rush
<me@tylerlogic.com>
September 12, 2014
http://coursework.tylerlogic.com/courses/upenn/math508/homework02
1 Density of rationals in reals
(a) For a ∈ ℚ with a > 0 and a2 < 2 find rational b > a with a2 < b2 < 2
First, if a < 1, then we can simply let b = 1 since a2 < 12 < 2 in this case. So
assume that a ≥ 1. This implies 2a + 1 ≥ 3. Furthermore, this implies that 2 - a2 < 2 - a < 2, from which we conclude
2 - a2 < 2a + 1. Thus, defining t = 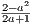 , means that 0 < t < 1.
, means that 0 < t < 1.
With this definition of t, setting b = a + t we see b2 = (a + t)2 = a2 + 2at + t2 < a2 + 2at + t where the last inequality
comes from the fact that 0 < t < 1. Continuing, we have
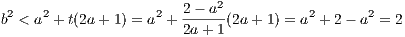
Thus since b = a + t and both a and t are positive, we have a2 < b2 < 2. Finally, t is rational since it is constructed by a
combination of multiplication and addition of rational numbers; this implies that rationality of b since it is the sum of two
rationals, a and t.
(b) For c ∈ ℚ with c > 0 and 2 < c2, find rational d > 0 with d < c and 2 < d2 < c2
Define t = 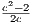 . Since 0 < c < 2 < c2 then
. Since 0 < c < 2 < c2 then
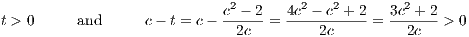
Now let d = c - t. The above equations imply that 0 < d < c and also allow for the use of the inequality in the following
equation.
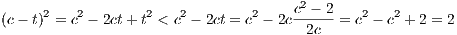
Given this equation, we now have 2 < d2 < c2, and furthermore, since d is equal to some combination of rational numbers
which are added/multiplied together, then it too is rational.
(c)
2 Some properties of an ordered field.
Let F be an ordered field containing elements x and y.
(a) Show that x < y implies x < 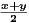 < y
< y
Let x < y. Then the definition of an ordered field and Rudin’s Proposition 1.18
yield x + x < x + y, implying 2x < x + y and thus x < 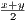 . Similarly we have obtain x + y < y + y, x + y < 2y, and
. Similarly we have obtain x + y < y + y, x + y < 2y, and
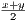 < y. Combining these results we have
< y. Combining these results we have
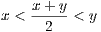
as desired.
(b) Prove x≠0 implies x2 > 0
First suppose x > 0. Then Rudin’s Proposition 1.18 (b) implies x(x) > x(0) which
is equivalent to x2 > 0.
Now suppose x < 0. Rudin’s Proposition 1.18 (c) implies x(x) > x(0), i.e. x2 > 0.
(c) Prove x2 + y2 = 0 implies x = y = 0
Lemma 2.1. If F is some ordered field and a,b ∈ F are such that a > 0 and b > 0, then a + b > 0.
Proof. Let F be an ordered field with a,b ∈ F such that a > 0 and b > 0. Adding b to the both sides of a > 0 yields
a + b > b, but b > 0, so a + b > 0. __
Let x,y not be both identically zero. Without loss of generality, assume x≠0. The previous problem then implies x2 > 0.
So if y = 0, then x2 + y2 = x2 > 0. If y≠0, then the previous problem gives y2 > 0 which the above lemma then yields
x2 + y2 > 0. Hence, in any case, x2 + y2≠0.
(d) Show that 2xy ≤ x2 + y2. When does equality occur?
Part (b) of this problem implies that for any x,y we have (x - y)2 ≥ 0. Thus
x2 - 2xy + y2 ≥ 0, and therefore x2 + y2 ≥ 2xy, as desired.
When does equality occur?
Stepping backwards through this proof, we see that x2 + y2 = 2xy when (x - y)2 = 0. Then part (b) of this problem
implies that x - y = 0. Thus we have equality when x = y.
3 More rational density
(a) Show there is an irrational between rationals x < y
If x < y, then 0 < y -x. Hence the archimedean property of the reals yields an
integer n > 0 such that n(y - x) > 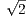 . Since
. Since  > 0 we have
> 0 we have
| 0 | < | 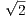 | < n(y - x) | | | |
|
| 0 | < | 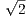 ∕n ∕n | < y - x | | | |
|
| x | < | x + 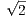 ∕n ∕n | < y | | | | |
Now we saw in the last homework that both the multiplication and sum of a rational with an irrational is irrational, so
x + 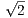 ∕n is irrational since
∕n is irrational since 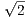 is irrational.
is irrational.
(b) Show there is a rational between any real numbers x < y
If x < y, then 0 < y -x. So again, the archimedean property gives us an integer
n > 0 such that ny -nx > 1. This implies, since consecutive integers have a difference of one, that there must some integer
m with nx < m < ny. Thus x < m∕n < y, and m∕n is rational.
4
5
(a) Find all sets A ⊂ ℝ such that sup A ≤ inf A
Let A ⊂ ℝ with a = inf A and bsupA. If x,y ∈ A and x < y then we would have
a ≤ x < y ≤ b, and so it’s not possible for a set with two or more elements to have a supremum that’s less than or equal to
the infimum. Hence only singleton sets have the desired property.
(b) If A ⊂ ℝ is bounded above and B ⊂ ℝ is bounded below, prove A ∩ B is bounded.
Let A ⊂ ℝ be bound above by α and B ⊂ ℝ be bounded below by β. Then a ≤ α
for all a ∈ A and β ≤ b for all b ∈ B, however, since A∩B ⊂ A and A∩B ⊂ B, then we must have that β ≤ x ≤ α for all
x ∈ A ∩ B. In other words, A ∩ B is bounded.
6
Let z,w,v ∈ ℂ be complex numbers.
(a) Prove |z - w|≥|z - v|-|v - w|.
We know for a,b ∈ ℂ that |a + b|≤|a| + |b|, which implies |a + b|-|b|≤|a|. Since
a and b are arbitrary, then we can find x,y ∈ ℂ when a = x - b and b = y, then |(x - y) + y|-|y|≤|x - y| which
implies
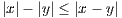
With this, we then have
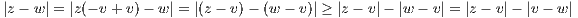
taking advantage of the fact that |x| = |- x| for all x ∈ ℂ in the rightmost equality.
(b) Graph the points z ∈ ℂ such that 1 < |z - i| < 2
The following region is the set of points, note that the edges of the region are not
included.
(c) For z,w ∈ ℂ with |z| < 1 and |w| = 1, prove |(w - z)∕(1 -zw)| = 1
We have the following sequence of equations due to the fact that |a| = |a|,
|ab| = |a||b|, |w| = 1, and a - b = a -b for any a,b ∈ ℂ.
7
Let x,y,z ∈ ℝ and define
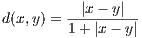
(a) Prove the above d(⋅,⋅) satisfies the triangle inequality
If |x - z|≤|y - z| or |x - z|≤|x - y|, then the fact that f(t) = t∕(1 + t) is an
increasing function implies the triangle inequality for d.
So assume that |x - z| is greater than both |x - y| and |y - z|. Since |x - z|≤|x - y| + |y - z| we have
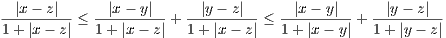
with the rightmost inequality comming from our initial assumption. Thus the triangle inequality holds for this
d(⋅,⋅).
(b)
The proof for this is identical to the proof of in the previous part of this problem
after substituting in the function |⋅-⋅| for g(⋅,⋅). This is because the only property of |⋅-⋅| that was used in the previous
proof was that it upholds the triangle inequality, which g(⋅,⋅) also does.
8
(a)
Let f1(x)∕f2(x),g1(x)∕g2(x) ∈ .
.
By the following, the zero constant is the additive identity:
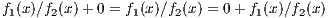
By the following, the one constant is the multiplicative identity:
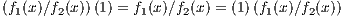
Then
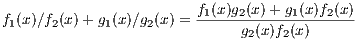
so 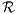 is closed under addition. Since polynomial addition is commutative and associative, then addition is commutative and
associative in
is closed under addition. Since polynomial addition is commutative and associative, then addition is commutative and
associative in 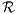 . Finally, since f(x) + (-f(x)) = 0, additive inverses exist in
. Finally, since f(x) + (-f(x)) = 0, additive inverses exist in 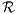 .
.
Since
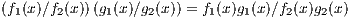
then 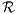 is closed under multiplication. Since polynomial multiplication is commutative and associative, then multiplication
is commutative and associative in
is closed under multiplication. Since polynomial multiplication is commutative and associative, then multiplication
is commutative and associative in 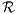 . Finally, if f1(x)∕f2(x) is not zero, then
. Finally, if f1(x)∕f2(x) is not zero, then
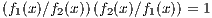
and so multiplicative inverses exist in 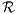 .
.
Finally, since polynomial addition and multiplication obides by the distributive law, then so does addition and
multiplication in 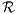 .
.
So 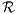 is indeed a field.
is indeed a field.
(b)
(c)
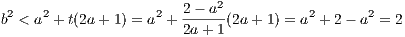
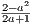 , means that 0 < t < 1.
, means that 0 < t < 1.
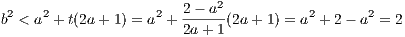
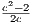 . Since 0 < c < 2 < c2 then
. Since 0 < c < 2 < c2 then
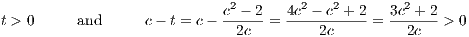
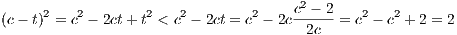
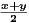 < y
< y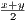 . Similarly we have obtain x + y < y + y, x + y < 2y, and
. Similarly we have obtain x + y < y + y, x + y < 2y, and
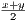 < y. Combining these results we have
< y. Combining these results we have
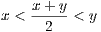
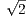 . Since
. Since  > 0 we have
> 0 we have
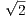
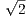 ∕n
∕n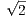 ∕n
∕n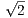 ∕n is irrational since
∕n is irrational since 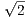 is irrational.
is irrational.
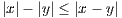
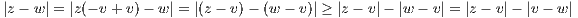

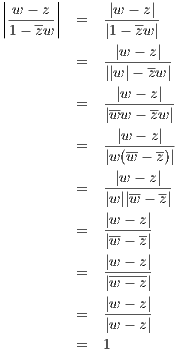
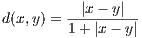
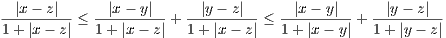
 .
.
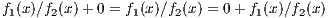
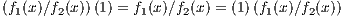
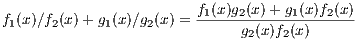
 is closed under addition. Since polynomial addition is commutative and associative, then addition is commutative and
associative in
is closed under addition. Since polynomial addition is commutative and associative, then addition is commutative and
associative in  . Finally, since f(x) + (-f(x)) = 0, additive inverses exist in
. Finally, since f(x) + (-f(x)) = 0, additive inverses exist in 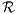 .
.
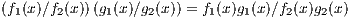
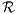 is closed under multiplication. Since polynomial multiplication is commutative and associative, then multiplication
is commutative and associative in
is closed under multiplication. Since polynomial multiplication is commutative and associative, then multiplication
is commutative and associative in 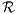 . Finally, if f1(x)∕f2(x) is not zero, then
. Finally, if f1(x)∕f2(x) is not zero, then
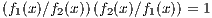
 .
.
 .
.
 is indeed a field.
is indeed a field.