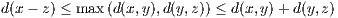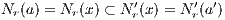Math 508: Advanced Analysis
Homework 3
Lawrence Tyler Rush
<me@tylerlogic.com>
September 19, 2014
http://coursework.tylerlogic.com/courses/upenn/math508/homework03
1 Give an example of closed sets V j ⊂ ℝ where ∪j=1∞V j is open.
Define V j = [-j,j]. Then ∪j=1∞V j = ℝ and ℝ is open. But this example leaves a bad
taste in one’s mouth since the union of the {V j} is the whole space, ℝ. As for a more slick example, define
V j = [-(1 - 1∕j),1 - 1∕j]. In this case ∪j=1∞V J = (-1,1), which is open in ℝ.
2 Construct a bounded set of real numbers with exactly three limit points
Define
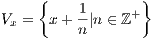
With this definition, x is the only limit point of V x and is bounded since it is contained within the ball B1(x). Therefore
V 1 ∪ V 2 ∪ V 3 is a bounded set with exactly three limit points.
3 Find the interior points and boundary points of each set, and describe the sets closure
(a) (0, 1] ⊂ ℝ
Interior points: (0,1)
Boundary points: {0,1}
Closure: [0,1]
(b) ℝ2 ⊂ ℝ3 (the coordinate plane z = 0)
Interior points: There are no interior points because there is no ball of any
point completely contained in the plane.
Boundary points: The set itself is the set of boundary points.
Closure: This set is closed, so the closure is itself.
(c) ℚ ⊂ ℝ
Interior points: There are no interior points. The set is countable, and therefore
discrete, so no neighborhood of any point can be completely contained within ℝ.
Boundary points: ℝ
Closure: ℝ
(d)
The graph of the function

as a subset of ℝ2. Call the set G.
Interior points: There are no interior points.
Boundary points: G ∪{(0,y) | |y|≤ 1}
Closure: Same as the boundard points.
4 Which sets are compact? Why?
(a) [0, 1] ⊂ ℝ
This set is a closed and bounded subset of ℝ, so it’s compact by
Heine-Borel.
(b) {0}∪{1, ,…,
,…, ,…}⊂ ℝ
,…}⊂ ℝ
Again, this set is a closed and bounded subset of ℝ, so it’s compact by
Heine-Borel.
(c) X=[0, 1] \ ℚ as a subset of ℝ
Since X contains no rational numbers then 0 ⁄∈ X, however, every open ball of
zero will contain a point of X since it will contain an irrational in [0,1]. Therefore 0 is a limit point of X, but since it’s not
contained in X, X is not closed. Because X is not closed as a subset of ℝ then it is not compact, again by
Heine-Borel.
5
For any element xk ∈ S we have that
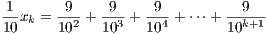
so
which gives us a closed form for each xk ∈ S. With this formula, it’s obvious that 1 is an upper bound. Assume for later
contradiction that there exists an a < 1 where a is an upper bound. However, for any integer k > -log 10(1 - a) we
have
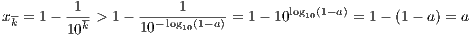
which contradicts our assumption that a is an upper bound. Thus 1 is the supS.
6
Define 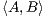 for A,B ∈
for A,B ∈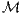 k,n by
k,n by 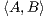 = trace(ABt)
= trace(ABt)
(a) Show this 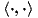 is an inner product.
is an inner product.
-
Positive Definite
- Let A ∈
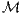 k×n with r1,r2,…,rk being the k vectors that make up the rows of A. Then
k×n with r1,r2,…,rk being the k vectors that make up the rows of A. Then
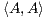 = trace(AAt) = r1r1t +r2r2t +
= trace(AAt) = r1r1t +r2r2t + +rkrkt. Since each ririt is simply the dot product of ri with itself,
then each ririt ≥ 0 with equality when ri is the zero vector. Thus
+rkrkt. Since each ririt is simply the dot product of ri with itself,
then each ririt ≥ 0 with equality when ri is the zero vector. Thus 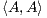 ≥ 0 with equality when A is the
zero matrix.
≥ 0 with equality when A is the
zero matrix.
-
Additivity
- Let A,B,C ∈
 k×n. By properties of the trace function and matrix multiplication we have
k×n. By properties of the trace function and matrix multiplication we have
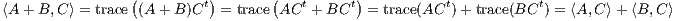
-
Homogeneity
- Let A,B ∈
 k×n and α ∈ ℝ. By properties of the trace function we have
k×n and α ∈ ℝ. By properties of the trace function we have
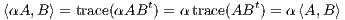
-
Symmetry
- Let A,B ∈
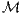 k×n. By properties of the trace function we have
k×n. By properties of the trace function we have
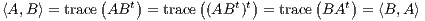
(b) Let |A|2 =  and define d(A,B) := |A - B|. Show d is a metric.
and define d(A,B) := |A - B|. Show d is a metric.
-
Non-negativity
-
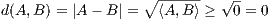
-
Symmetry
-
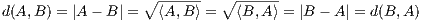
-
Triangle Inequality
-
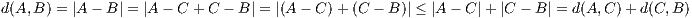
(c)
(d)
7
Let K be compact in ℝn with x ⁄∈ K. Further let d = inf{d(x,y) | y ∈ K}. There
must be a limit point z ∈ ℝn of K such that d(x,z) = d, If there were not such a point, then we’d be able to find
some r > 0 such that Br(p) ∩ K = {} for p with d(x,p) = d. This would imply that, say, d + 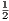 r would be a
lower bound on the set {d(x,y) | y ∈ K}, which is a contradiction since d is the infimum of that set. Now
because z is a limit point of K and K is compact, then it is also closed by Heine-Borel. Hence z ∈ K, as
desired.
r would be a
lower bound on the set {d(x,y) | y ∈ K}, which is a contradiction since d is the infimum of that set. Now
because z is a limit point of K and K is compact, then it is also closed by Heine-Borel. Hence z ∈ K, as
desired.
8
Let X = ℝ -{0} with the normal metric on ℝ of the absolute value of
the difference between two points. Then the sets A = [-1,0) and B = (0,1] are closed sets since zero is
not in X. They are obviously dijsoint. Furthermore dist(A,B) = 0 since each has points arbitrarily close to
zero.
9
Let {xn} be a sequence of points in ℝ2 that contains every point with rational
coordinates. Let {rn} be a sequence of positive real numbers such that ∑
nrn = 1. Define
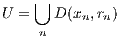
where D(x,r) is the disc of radius r centered at x.
(a) Show U is open and dense in ℝ
The set U is open because it is the union of open sets. Also, the set U is dense in
ℝ2 because ℚ2 is dense in ℝ2 and U contains ℚ2 as a subset.
(b) Show that no straight line L is completely contained in U
Let L be a line in the plane. A line is the linear combination of two specified
points, so let those points be u and v. Then L is the set of points (1 - c)u + cv = u + c(v - u) for all c ∈ ℝ.
By way of contradiction, assume that L is completely contained in U. Then for any n ∈ ℕ, we have that
D(xn,rn) ∩ L = {u + c(v - u) | c ∈ (sn,tn)} for some sn,tn ∈ ℝ. Thus by defining the function f : L → ℝ by
f(u + c(v - u)) = c we see that f(D(xn,rn) ∩ L) = (sn,tn). So for all n ∈ ℕ, we get an open cover of the real line. For
instance, we can cover the closed interval [0,3], but since [0,3] is compact, we can find a finite open subcover
(sn1,tn1),…,(snk,tnk). However, this implies that
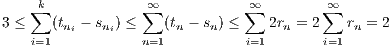
and we thus arrive at a contradiction. Hence L is not completely contained in U.
10 Product Topology
Let (E1,d1) and (E2,d2) be two metric spaces and define the distance on E1 ×E2 to
be
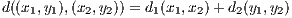
for each (x1,y1),(x2,y2) ∈ E1 × E2.
(a) Warmup
Viewing ℝ2 as ℝ × ℝ we have

and the “disc” centered at the origin is
(b)
Let U ⊂ E1 × E2 be an open subset. Let (u1,u2) ∈ U. We can thus
find an open ball Br(u1,u2) ⊂ U. Define U1 = {x ∈ E1 | d((x,u2),(u1,u2)) < r}. With this definition for
any x ∈ U1, the open ball of radius 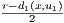 will be contained in U1 since any y ∈ B
will be contained in U1 since any y ∈ B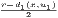 (x) has that
so that d((y,u2),(u1,u2)) < r. Thus U1 is open in E1. Similarly, we also have that the set U2 = {x ∈ E2 | d((u1,x),(u1,u2)) < r}
is open in E2 because each x ∈ U2 has the open ball B
(x) has that
so that d((y,u2),(u1,u2)) < r. Thus U1 is open in E1. Similarly, we also have that the set U2 = {x ∈ E2 | d((u1,x),(u1,u2)) < r}
is open in E2 because each x ∈ U2 has the open ball B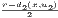 (x) around it which is completely contained in U2. Finally,
with the simple definitions of U1 and U2, we see (u1,u2) ∈ U1 × U2 and U1 × U2 ⊂ Br(u1,u2) ⊂ U, as
desired.
(x) around it which is completely contained in U2. Finally,
with the simple definitions of U1 and U2, we see (u1,u2) ∈ U1 × U2 and U1 × U2 ⊂ Br(u1,u2) ⊂ U, as
desired.
Conversely, assume that for each point (u1,u2) ∈ U there exist U1, U2 open in E1, E2, respectively, with
(u1,u2) ∈ U1 × U2 and U1 × U2 ⊂ U. So fix (u1,u2) ∈ U. As a consequence of the hypothesis at the opening of this
paragraph, we can find open balls Br1(u1) ⊂ U1 and Br2(u2) ⊂ U2. Define r = min(r1,r2). Then for any point
(x,y) ∈ Br((u1,u2)) we have
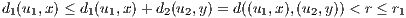
and
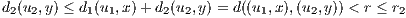
which implies x ∈ Br1(u1) and y ∈ Br2(u2), respectively. In turn, this means (x,y) ∈ U1 ×U2 and thus (x,y) is also in U.
Hence the open ball Br((u1,u2)) is contained in U, i.e. U is open.
11 The p-adic topology on the rational numbers.
(a) Show that (ℚ,dp) is a metric space.
Fix a prime p.
Lemma 11.1. For x,y,z ∈ ℚ, d(x,z) ≤ max(d(x,y),d(y,z)).
Proof. Let x,y,z be rational numbers. Then we have
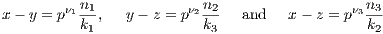
where p does not divide any ni or ki. With this in place we assume without loss of generality that ν1 ≤ ν2 so that
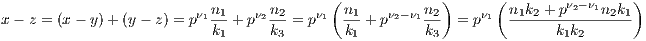
Now with both the above and below forms of x - z, we see ν3 ≥ ν1, which given our assumption that ν1 ≤ ν2,
implies ν3 ≥ min(ν1,ν2). Hence we have
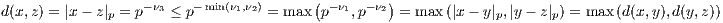
as desired. __
-
Non-negativity
- Let x,y ∈ ℚ be distinct. Then d(x,y) = |x-y|p = p-ν for some ν. Since p is positive, then d(x,y)
will always be positive. On the other hand d(x,x) = |x - x|p = 0.
-
Symmetry
- Let x,y ∈ ℚ with x - y = pν
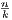 . Then y - x = pν
. Then y - x = pν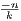 , implying that |x - y|p = |y - x|p = p-ν. Hence
d(x,y) = d(y,x).
, implying that |x - y|p = |y - x|p = p-ν. Hence
d(x,y) = d(y,x).
-
Triangle Inequality
- Let x,y,z ∈ ℚ. Making use of the lemma above, we obtain
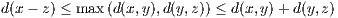
(b) For x,a ∈ ℚ show that x ∈ Nr(a) implies Nr(x) = Nr(a).
Let x,y,a ∈ ℚ with r > 0 and x ∈ Nr(a). Then d(x,a) < r.
So for any y ∈ Nr(x), d(x,y) < r. In particular, d(y,a) ≤ max(d(x,a),d(x,y)) < max(r,r) = r, by the above lemma. So
y ∈ Nr(a), i.e. Nr(x) ⊂ Nr(a).
On the other hand, we similarly have that for any y ∈ Nr(a), d(y,a) < r and therefore d(x,y) ≤ max(d(x,a),d(a,y)) < max(r,r) = r
again by the above lemma. Thus y ∈ Nr(x), meaning Nr(a) ⊂ Nr(x).
Combining these two results leaves us with Nr(x) = Nr(a).
(c) Show that any two neighborhoods are disjoint, or one is contained in the other.
Let a,a′∈ ℚ and r,r′ be positive reals. If Nr(a) and Nr′(a′) are disjoint, we are
done. So assume not. Then there is an x ∈ Nr(a) ∩ Nr′(a′). By the previous part of the problem, we then
have Nr(x) = Nr(a) and Nr′(x) = Nr′(a′). Thus by assuming without loss of generality that r < r′ we
obtain
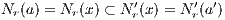
as desired.
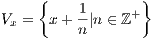
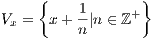

 ,…,
,…,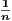 ,…}⊂ ℝ
,…}⊂ ℝ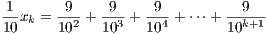
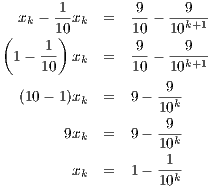
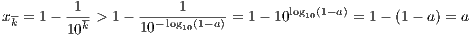
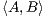 for A,B ∈
for A,B ∈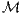 k,n by
k,n by 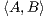 = trace(ABt)
= trace(ABt)
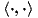 is an inner product.
is an inner product.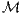 k×n with r1,r2,…,rk being the k vectors that make up the rows of A. Then
k×n with r1,r2,…,rk being the k vectors that make up the rows of A. Then
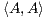 = trace(AAt) = r1r1t +r2r2t +
= trace(AAt) = r1r1t +r2r2t + +rkrkt. Since each ririt is simply the dot product of ri with itself,
then each ririt ≥ 0 with equality when ri is the zero vector. Thus
+rkrkt. Since each ririt is simply the dot product of ri with itself,
then each ririt ≥ 0 with equality when ri is the zero vector. Thus 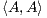 ≥ 0 with equality when A is the
zero matrix.
≥ 0 with equality when A is the
zero matrix.
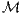 k×n. By properties of the trace function and matrix multiplication we have
k×n. By properties of the trace function and matrix multiplication we have
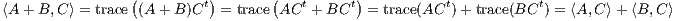
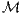 k×n and α ∈ ℝ. By properties of the trace function we have
k×n and α ∈ ℝ. By properties of the trace function we have
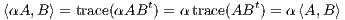
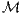 k×n. By properties of the trace function we have
k×n. By properties of the trace function we have
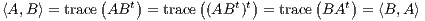
 and define d(A,B) := |A - B|. Show d is a metric.
and define d(A,B) := |A - B|. Show d is a metric.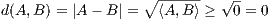
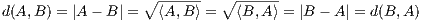
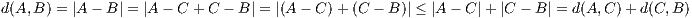
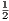 r would be a
lower bound on the set {d(x,y) | y ∈ K}, which is a contradiction since d is the infimum of that set. Now
because z is a limit point of K and K is compact, then it is also closed by Heine-Borel. Hence z ∈ K, as
desired.
r would be a
lower bound on the set {d(x,y) | y ∈ K}, which is a contradiction since d is the infimum of that set. Now
because z is a limit point of K and K is compact, then it is also closed by Heine-Borel. Hence z ∈ K, as
desired.
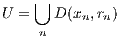
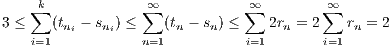
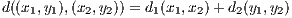


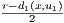 will be contained in U1 since any y ∈ B
will be contained in U1 since any y ∈ B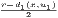 (x) has that
(x) has that
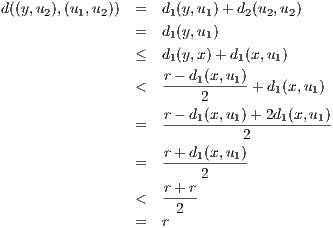
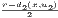 (x) around it which is completely contained in U2. Finally,
with the simple definitions of U1 and U2, we see (u1,u2) ∈ U1 × U2 and U1 × U2 ⊂ Br(u1,u2) ⊂ U, as
desired.
(x) around it which is completely contained in U2. Finally,
with the simple definitions of U1 and U2, we see (u1,u2) ∈ U1 × U2 and U1 × U2 ⊂ Br(u1,u2) ⊂ U, as
desired.
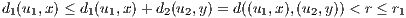
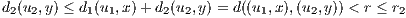
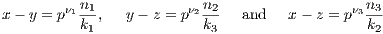
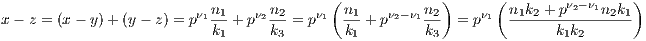
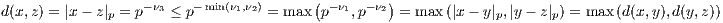
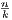 . Then y - x = pν
. Then y - x = pν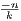 , implying that |x - y|p = |y - x|p = p-ν. Hence
d(x,y) = d(y,x).
, implying that |x - y|p = |y - x|p = p-ν. Hence
d(x,y) = d(y,x).