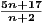
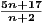
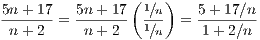
Since 1∕n → 0 then 17∕n → 0 and 2∕n → 0. Therefore 5 + 17∕n → 5 and 1 + 2∕n → 1. Thus 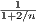 → 1 implying that
→ 1 implying that
 → 5. Given the opening equation, this then final implies
→ 5. Given the opening equation, this then final implies

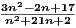
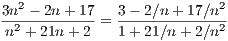
Since 1∕n → 0, then 1∕n2 → 0. This implies 3 - 2∕n + 17∕n2 → 3 and 1 + 21∕n + 2∕n2 → 1. Hence 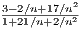 converges
to three and thus so does
converges
to three and thus so does  , as per the opening equation.
, as per the opening equation.
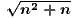 - n
- n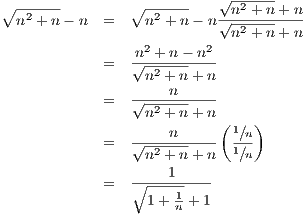
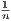 → 0 so that 1 +
→ 0 so that 1 + 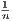 → 1. Since 1 < 1 +
→ 1. Since 1 < 1 + 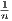 , then 1 <
, then 1 < 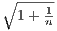 < 1 +
< 1 + 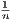 , which means that
, which means that
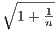 → 1 by the “squeeze theorem” in problem 6. It follows that
→ 1 by the “squeeze theorem” in problem 6. It follows that 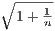 + 1 → 2, from which which
see
+ 1 → 2, from which which
see
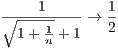
Hence, given the opening equation of this problem, we have 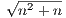 - n →
- n →
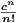 for c > 0
for c > 0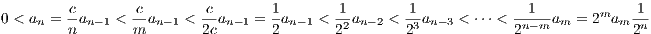
Thus limn→∞an ≤ 2mam limn→∞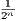 = 0
= 0
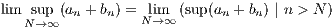
but for any integer N, 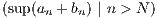 ≤
≤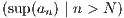 +
+ 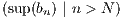 so that
so that
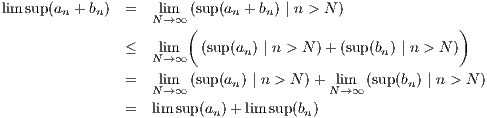
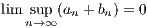
where as
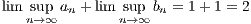
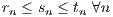 | (6.1) |
Assume that both tn → s and rn → s. Then for any r > 0, there is are integers N1,N2 such that rn,tn ∈ B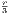 (s) for all
n ≥ N where N = max(N1,N2). Therefore |rn - tn| <
(s) for all
n ≥ N where N = max(N1,N2). Therefore |rn - tn| < 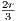 which, combined with equation 6.1, implies |sn - tn| <
which, combined with equation 6.1, implies |sn - tn| < 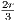 for
each n ≥ N. Therefore
for
each n ≥ N. Therefore

for each n ≥ N. Hence Br(s) contains all but finitely many points in {sn}, so that sn → s.
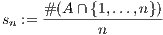
be the fraction of natural numbers from one to n which are not divisible by three. Thus defining the sequence {tn} where tn is the fraction of natural numbers less than or equal to n that are divisibile by three, we have
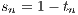 | (7.2) |
for each n. Now tn = 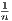
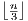 , which implies tn ≤
, which implies tn ≤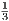 for each n. Thus for any ε > 0 we have
for each n. Thus for any ε > 0 we have
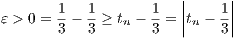
so that tn →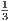 . Thus due to Equation 7.2, sn →
. Thus due to Equation 7.2, sn →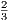 .
.
Repeat this for all natural numbers not multiples of two or three
Let {tn} again be as above, the fraction of natural numbers less than or equal to n which are divisible by three. Define
{rn} as the sequence where each rn is the fraction of natural numbers less than or equal to n which are divisible by two.
Thus we have rn = 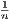
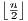 , which with an argument nearly identical to the one for {tn} converging to
, which with an argument nearly identical to the one for {tn} converging to 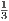 above, we know
rn →
above, we know
rn →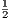 . If, now, the sequence {an} is such that each an is the fraction of natural numbers less than or equal to n which are
not divisible by two or three, we have
. If, now, the sequence {an} is such that each an is the fraction of natural numbers less than or equal to n which are
not divisible by two or three, we have
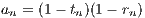
Hence an converges to 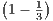
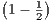 =
= 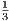 since tn and rn converge to
since tn and rn converge to 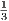 and
and 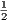 , respectively.
, respectively.
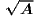
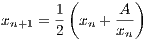
We note that for the real-valued function f(x) = 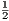
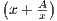 we have f′(x) =
we have f′(x) = 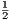
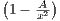 . Thus f′(x) = 0 when x =
. Thus f′(x) = 0 when x = 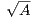 ,
implying that f(
,
implying that f(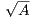 ) =
) = 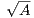 is the minimum value of f. Since {xn} are just particular values of f, then {xn} is bounded
below by
is the minimum value of f. Since {xn} are just particular values of f, then {xn} is bounded
below by 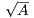 .
.
So let’s define a sequence {yn} by yn = xn -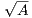 . Then we have
. Then we have
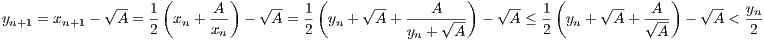
This then indicates that yn+1 < 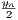 <
<  <
< 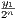 which in turn implies that yn → 0. Since we defined yn = xn -
which in turn implies that yn → 0. Since we defined yn = xn -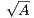 , then
xn = yn +
, then
xn = yn + 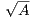 yielding xn →
yielding xn →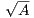 .
.
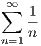
diverges. This implies that
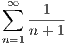 | (9.3) |
also diverges since it’s one less than the first. We use this fact to our advantage in finding a counter-example. Define the sequence {an} by recursively by a0 = 0 and
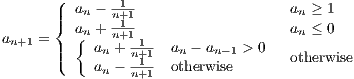
This sequence essentially bounces back and forth between zero and one, so is bounded. It also satisfies the property that
|an -an-1| < 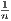 since each point an differs by
since each point an differs by 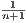 from the previous. Furthermore, we know once the sequence “hits” one
and heads back to zero (and vice versa), that it will actually reach zero because of the divergence of 9.3 above; i.e. starting
at zero but not being able to reach one (and vice versa) at any point in the sequence would imply convergence of
9.3.
from the previous. Furthermore, we know once the sequence “hits” one
and heads back to zero (and vice versa), that it will actually reach zero because of the divergence of 9.3 above; i.e. starting
at zero but not being able to reach one (and vice versa) at any point in the sequence would imply convergence of
9.3.
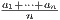 , i.e. {cn} is the sequence of
partial averages of {an}.
, i.e. {cn} is the sequence of
partial averages of {an}.
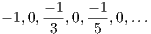
converging to zero.
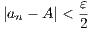 | (10.4) |
Furthermore, because {an} converges, it is bounded, so that we can find an integer M with
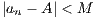 | (10.5) |
for all n. Thus for n > N we have
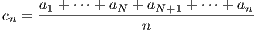
implying that
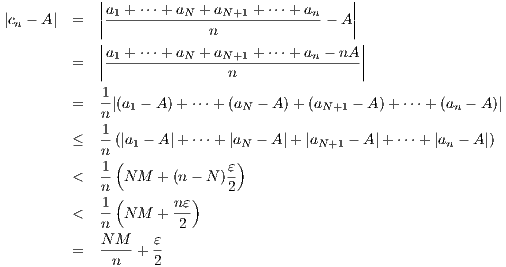
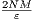 we have
we have
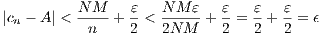
implying the convergence of {cn} to A.
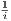 . We know that this series diverges, and so the sequence {an} must be unbounded. However, in this case {cn}
has
. We know that this series diverges, and so the sequence {an} must be unbounded. However, in this case {cn}
has
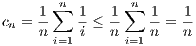
which implies cn → 0.