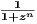 for complex z
for complex z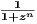 for complex z
for complex z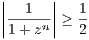
Therefore 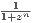 ⁄→ 0, implying the divergence of ∑
⁄→ 0, implying the divergence of ∑
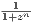 in this case.
in this case.
Now assume that |z| > 1. Then |zn| increases as n gets large and |zn + 1| > 2. So let N be such that |zn| > 2 for all n > N. Then
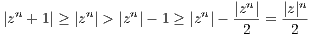 | (1.1) |
for all n > N. By separating ∑
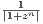 like so
like so
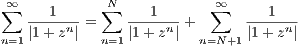
equation 1.1 informs us that
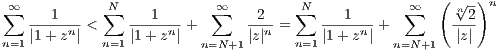
Now the left addend of the right-hand side of the above inequality is a finite sum and the right addend is a convergent
geometric series since 0 < 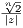 < 1. Thus the right-hand side of the above inequality converges, implying the convergence of
the left-hand side, ∑
n=1∞
< 1. Thus the right-hand side of the above inequality converges, implying the convergence of
the left-hand side, ∑
n=1∞ . This in turn implies that our series in question is absolutely convergent when |z| > 1, and
therefore convergent.
. This in turn implies that our series in question is absolutely convergent when |z| > 1, and
therefore convergent.
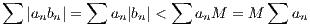
so due to the convergence of ∑ an, then M ∑ an and therefore ∑ |anbn| converges. Hence ∑ anbn converges absolutely, and so converges.
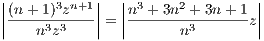
approaches z as n increases, then the ratio test tells us that the radius of convergence is 1.
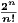 zn
zn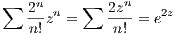
and so this series converges for all z, i.e. the radius is infinite.
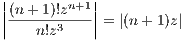
approaches ∞ as n increases, then the ratio test tells us that the radius of convergence is 0, but technically, z = 0 will make the series converge.
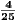 for n ≥ 1
for n ≥ 1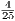 = 0
given the recursive definition. Therefore, L can only be
= 0
given the recursive definition. Therefore, L can only be  or
or 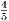 since these are the roots of that equation.
since these are the roots of that equation.
Now since a0 = 0, the recusive formula just adds a positive value of 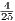 , informing us that this sequence if monotonically
increasing. Furthermore, if an <
, informing us that this sequence if monotonically
increasing. Furthermore, if an < 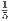 we see that
we see that

which simultaneously implies that the sequence is bounded and rules out 4∕5 as a possible limit. Thus the sequence is
monotonically increasing and bounded, implying that it must converge, and because the initial value is zero, the only point
it can converge to is 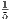 .
.
 converges
converges + an converge. This implies the convergence of {tn} where tn =
+ an converge. This implies the convergence of {tn} where tn = 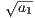 +
+  +
+ 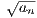 since each an ≥ 0. Thus
defining ∑
xn = ∑
since each an ≥ 0. Thus
defining ∑
xn = ∑
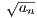 implies that {tn} is the sequence of partial sums of ∑
xn and they form a bounded sequence.
Furthermore, defining ∑
yn as the harmonic series, we have y0 ≥ y1 ≥ y2 ≥
implies that {tn} is the sequence of partial sums of ∑
xn and they form a bounded sequence.
Furthermore, defining ∑
yn as the harmonic series, we have y0 ≥ y1 ≥ y2 ≥ and limn→∞yn = 0. Thus Rudin’s Theorem
3.42 informs us that the series
and limn→∞yn = 0. Thus Rudin’s Theorem
3.42 informs us that the series
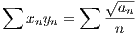
converges.
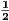 +
+ 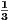 +
+ 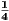 +
+  +
+  > 100
> 100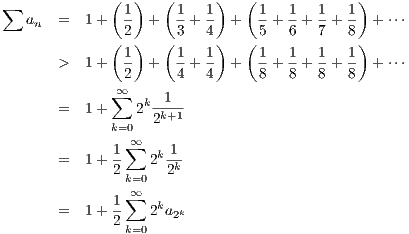
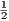 ∑
k=0K2ka2k > 100 then for N = 2K we’ll have 1 +
∑
k=0K2ka2k > 100 then for N = 2K we’ll have 1 + 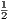 +
+ 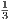 +
+ 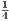 +
+  +
+ 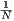 > 100. Thus since
> 100. Thus since
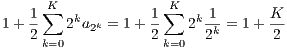
then 1 + 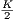 > 100 implies that K > 198, so K = 199 and therefore N = 2199 will satisfy.
> 100 implies that K > 198, so K = 199 and therefore N = 2199 will satisfy.
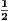 -
-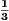 -
-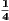 +
+ 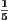 +
+ 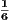 -
- converges
converges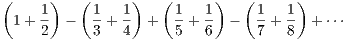
we see that it is no different than ∑ cn where
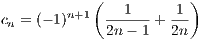
This is an alternating series for which 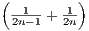 converges to zero, so our original series must also converge by Rudin’s
theorem 3.43.
converges to zero, so our original series must also converge by Rudin’s
theorem 3.43.
 + AN)
+ AN)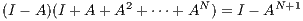
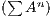 will be I and therefore
I - A will be invertibile. Since
will be I and therefore
I - A will be invertibile. Since
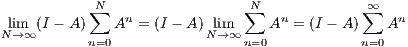
we’ll have that I -A is invertible if ∑ n=0∞An converges. Thus because ∑ |An|≤∑ |A|n, the right side converges since it’s a geometric series and |A| < 1. This tells us that ∑ An converges absolutely and that therefore ∑ An converges. Hence we have our desired result of I - A being invertible.
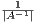 and B be a matrix in the ε-ball of A. Then we have that
|A-B| < ε implying that |A-1||A-B| < 1. Thus |I -A-1B| < 1. By the previous part of the problem, we then know that
I -
and B be a matrix in the ε-ball of A. Then we have that
|A-B| < ε implying that |A-1||A-B| < 1. Thus |I -A-1B| < 1. By the previous part of the problem, we then know that
I -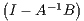 = A-1B is invertible. Then there is some invertible matrix C with CA-1B = I. But then B is invertible
with inverse CA-1. Hence the ε-ball of A contains only invertible elements, and so the set of invertible matrices is
open.
= A-1B is invertible. Then there is some invertible matrix C with CA-1B = I. But then B is invertible
with inverse CA-1. Hence the ε-ball of A contains only invertible elements, and so the set of invertible matrices is
open.
Bounded. Since any othogonal matrix A has that AAt = I, then with our definition of the norm, |A|2 = ⟨A,A⟩ = trace(AAt) = trace(I) = n. Thus the set of othogonal matrices is bounded.