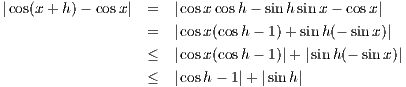
cos x is continuous: Let x ∈ ℝ For any |h| we have
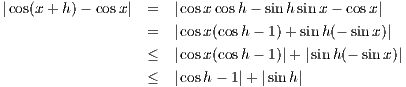
sin x is continuous: Let x ∈ ℝ For any |h| we have
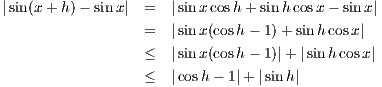
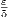 . Then 0 < δ < 1, given the constraints
on ε. Assume that |x| < δ, so that 0 < |x| < δ < 1, in particular 0 < |x|2 < |x| < 1. With this and the triangle inequality, we
then have
. Then 0 < δ < 1, given the constraints
on ε. Assume that |x| < δ, so that 0 < |x| < δ < 1, in particular 0 < |x|2 < |x| < 1. With this and the triangle inequality, we
then have
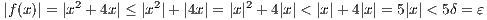
as desired.
Now let T : ℝ≥0 → ℝ be the function whose value at θ ∈ ℝ≥0 is the temperature of pθ. We will assume that this temperature function is continuous. Define the function D : ℝ≥0 → ℝ by D(θ) = T(θ) -T(θ + π), i.e. it is the difference in temperature of pθ and its diametrically opposite point, pθ+π. Since D is made up of the composition and difference of continuous functions, then it too is continuous.
Let pθ be a point on the equator that doesn’t have the same temperature as its diametric opposite (there must be such a point, otherwise there would be nothing to prove as all points diametrically opposite would have the same temperature). Then D(θ) = -D(θ + π) and neither values are zero. Without loss of generality, assume that D(θ) < 0 < D(θ + π). Since D is continuous and it’s domain, ℝ≥0, is connected, then this and the intermediate value theorem implies that there is a θ′∈ (θ,θ + π) such that D(θ′) = 0. But this implies that T(θ′) = T(θ′ + π), i.e. the diametrically opposed points pθ′ and pθ′+π have the same temperature.
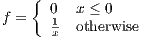
has the desired property of f(an) → 0 and f(bn) being unbounded.
Does there exist such a function that’s continuous at x = 0 This is not possible as it would contradict Rudin’s Theorem 4.2.
For constant a how does f(a,n) behave as n →∞? When a is constant, 1 + a > 1 since a was assumed positive. So f(a,n) = (1 + a)n →∞ as n →∞.
For constant n how does f(a,n) behave as a → 0? As a → 0, 1 + a → 1. So for constant n, f(a,n) = (1 + a)n → 1 as a → 0.
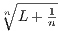 - 1, then an is a sequence of positive values, and
furthermore
- 1, then an is a sequence of positive values, and
furthermore
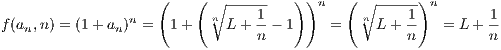
so that f(an,n) → L as n →∞.
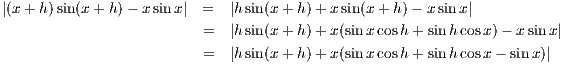
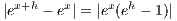
so no matter the value of h, |ex(eh - 1)| can be made arbitrarily large, and therefore so can |ex+h -ex|. Hence ex cannot be uniformly continuous on [0,∞)
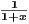
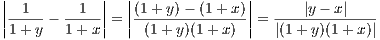
Since x,y ∈ [0,∞) then 1 + y ≥ 1 and 1 + x ≥ 1 which implies
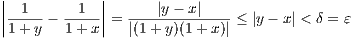
so that f(x) is uniformly continuous on [0,∞)
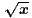 is continuous ∀x ≥ 0
is continuous ∀x ≥ 0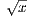 so that in particular ε =
so that in particular ε = 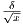 . Then for any
y ≥ 0 such that |x - y| < δ we have
. Then for any
y ≥ 0 such that |x - y| < δ we have

indicating that f is continuous at x.
Is the function uniformly continuous?
Yes. First note that because f is continous, as per above, then because [0,1] is compact in ℝ f is uniformly continuous
on [0,1]. Furthermore, for any x,y ∈ [1,∞), 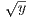 +
+ 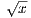 ≥ 1. Therefore for any ε > 0, setting δ = ε means that when
|y - x| < δ we have
≥ 1. Therefore for any ε > 0, setting δ = ε means that when
|y - x| < δ we have
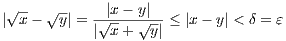
so that f is uniformly continuous on [1,∞).
Finally for any ε > 0, define δ = min(δ-,δ+) where δ- is such that |x-y| < δ-⇒|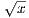 -
-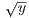 | <
| < 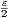 for all x,y ∈ [0,1] and
δ+ is such that |x - y| < δ+ ⇒|
for all x,y ∈ [0,1] and
δ+ is such that |x - y| < δ+ ⇒|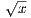 -
-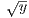 | <
| < 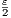 for all x,y ∈ [1,∞). Thus with this definition, whether x,y ∈ [0,1] or
x,y ∈ [1,∞), |x - y| < δ will imply |
for all x,y ∈ [1,∞). Thus with this definition, whether x,y ∈ [0,1] or
x,y ∈ [1,∞), |x - y| < δ will imply |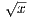 -
-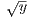 | < ϵ.
| < ϵ.
It remains to be seen that |x-y| < δ implies |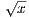 -
-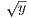 | < ϵ when x ∈ [0,1] and y ∈ [1,∞). This nevertheless holds, since
for x ∈ [0,1] and y ∈ [1,∞), |x - y| < δ implies both |x - 1| < δ < δ- and |y - 1| < δ < δ+. These two equations in turn
imply |
| < ϵ when x ∈ [0,1] and y ∈ [1,∞). This nevertheless holds, since
for x ∈ [0,1] and y ∈ [1,∞), |x - y| < δ implies both |x - 1| < δ < δ- and |y - 1| < δ < δ+. These two equations in turn
imply |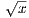 -
-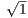 | <
| <  and |
and |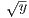 -
-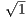 | <
| < 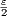 . Hence we obtain
. Hence we obtain
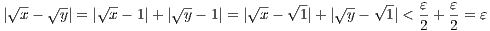
Therefore f is uniformly continous on all of [0,∞).
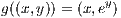
will also be a homeomorphism.
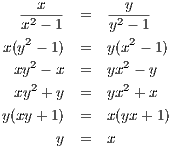
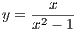
then we’d have
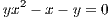
and the quadratic formula yields
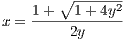
as one of the roots. Thus because

then we have a solution for x < 1. Thus f is a homeomorphism.

Let ε > 0 and set δ = ε. The for |x| < δ we have
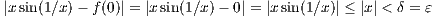
so that f is continuous at zero.
 + f(1) = nf(1) = nc. Thus for any rational n∕m we
have
+ f(1) = nf(1) = nc. Thus for any rational n∕m we
have
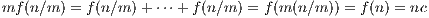
so that f(n∕m) = (n∕m)c. Thus any rational q ∈ ℚ has f(q) = qc. With this, we finally have that for x ∈ ℝ and a rational sequence {an} with an → r, the continuity of f yields
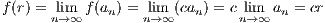
as desired.
Proof. Let E be a bounded subset of a metric space X, and x,y two points of its closure, E. If x,y ∈ E, then there’s nothing to prove since E is already bounded. We must address two remaining case:
Assume the first, and without loss of generality, let x ∈ E and y be a limit point of E. Then any open ball centered at y, say B1(y), contains some point of x ∈ E. Thus d(x,y) ≤ d(x,x) + d(x,y) < M + 1 where M is a bound for the set E. Hence the distance between any point of E and a limit point is bounded.
Now assume the second case above. By the previous paragraph we have d(x,y) ≤ d(x,z) + d(z,y) < 2(M + 1) for any z ∈ E. So in this case, the distance is bounded.
Hence we have that the closure of E is bounded. __
Let E ⊂ ℝ be a bounded set. Then the closure, E, is also bounded by the above lemma. Hence it’s closed and bounded, implying that it’s compact as a subset of ℝ. Therefore, the set f(E) is also compact since f is continuous. Thus f(E) is bounded since it’s a subset of ℝ. But because E ⊂E, then f(E) ⊂ f(E), and so f(E) must also be bounded.