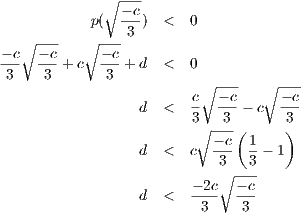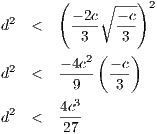Math 508: Advanced Analysis
Homework 7
Lawrence Tyler Rush
<me@tylerlogic.com>
November 1, 2014
http://coursework.tylerlogic.com/courses/upenn/math508/homework07
1 Prove that smooth f : [a,∞) → ℝ with bound first derivative is uniformly continuous.
Let f : [a,∞) → ℝ be smooth with M bound the first derivative, i.e. |f′(x)|≤ M. Let
ε > 0 and set δ = ε ∕ M. Then for any x,y ∈ [a,∞), assuming without loss of generality that x < y, the mean value theorem
informs us of a c ∈ (x,y) such that
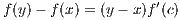
Hence if |y - x| < δ, we have

so that f is uniformly continuous.
2
(a) Show that sin x is not a polynomial.
The function sinx is zero at 2πn for all integers n, i.e. it has infinitely many
zeros. Polynomials have a finite amount of zeros, and so sinx cannot be a polynomial.
(b) Show that sin x cannot be a rational function.
A rational function p(x)∕q(x) is zero if and only if p(x) is zero. Therefore a
rational function is zero at only finitely many points, and just as we saw in the previous part of the problem, this implies
sinx cannot be a rational function.
(c) If f(t + 1) = f(t) for all real t, and f is not constant, show that f is not a rational function.
By way of contradiction, assume that f is a rational polynomial so that
f(t) = p(t)∕q(t). Fixing t0 ∈ ℝ and by putting g(t) = f(t) - f(t0) we have
- g(t + 1) = f(t + 1) - f(t0) = f(t) + f(t0) = g(t) so that g is periodic
- g(t) = p(t)∕q(t) - f(t0) =
 so that g is rational, and
so that g is rational, and
- g(t0) = f(t0) - f(t0) = 0 so that g has a zero at t0.
Putting the above three things together informs us that g is a rational function with infinitely many zeros, but rational
functions can only have a finite number of zeros; a contradiction.
(d) Show that ex is not a rational function.
A rational function f(x) has that
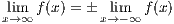
however
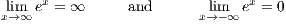
3 Show that lim n→∞(n + 1)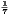 - n
- n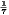 = 0
= 0
Define f : ℝ → ℝ by f(x) = x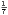 . Since this is a polynomial, it’s smooth on ℝ. For an
integer n, the mean value theorem tells us that there is an x ∈ (n,n + 1) such that
. Since this is a polynomial, it’s smooth on ℝ. For an
integer n, the mean value theorem tells us that there is an x ∈ (n,n + 1) such that

which in turn yields
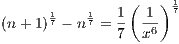
Hence
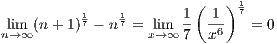
as desired.
4
Let f : ℝ → ℝ be smooth with f(0) = 3, f(1) = 2, and f(3) = 8. The Mean Value
Theorem yields the existence of c1 ∈ (0,1) and c2 ∈ (1,3) such that and Because f is smooth, f′ is continous since f′′ is differentiable, and thus we can appeal to the Mean Value Theorem again to
obtain a c ∈ (c1,c2) such that Since c2 > c1 > 0 this implies f′′(c) > 0, as desired. Furthermore, because, more precisely, 3 > c2 > 1 > c1 > 0 we have that
3 > c2 - c1 so that f′′(c) >  according to the above equation. So let M =
according to the above equation. So let M = 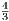 .
.
5
By “a convex function f” we mean one for which every point of the graph of f lies
above all of its tangent points; i.e. one for which
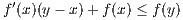
for all x,y ∈ ℝ.
(a) Show that a smooth function f is convex if f′′(x) ≥ 0 for all x.
Assume that the second derivative of f is non-negative for any point of ℝ. For
any reals x,y with x < y the Mean Value Theorem (MVT) gives us a z ∈ (x,y) such that
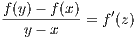 | (5.1) |
Since f is smooth, f′ is differentiable on [x,z], and so the MVT gives us a w ∈ (x,z) such that
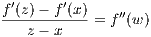
Since the second derivative is non-negative, then so is the left hand side of the above equation. Since z > x this implies
f′(z) ≥ f′(x) which in light of Equation 5.1 implies 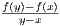 ≥ f′(x). This yields
≥ f′(x). This yields
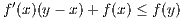
as desired for the convexity of f.
(b) Prove that v(x) ≤ 0 for all 0 ≤ x ≤ 1 if v′′(x) > 0 for 0 ≤ x ≤ 1 and v(0) = v(1) = 0
Assume for later contradiction that there is a point x ∈ (0,1) with v(x) > 0. Then
there exists a c1 ∈ (0,x) with
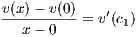
by the MVT so that 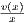 = v′(c1) which implies v′(c1) > 0 since v(x) > 0. Furthermore there exists an c2 ∈ (x,1)
where
= v′(c1) which implies v′(c1) > 0 since v(x) > 0. Furthermore there exists an c2 ∈ (x,1)
where
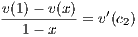
so that 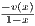 = v′(c2). Since x < 1 and v(x) > 0, then v′(c2) < 0. Once more, the MVT tells us there exists a c ∈ (c1,c2)
such that
= v′(c2). Since x < 1 and v(x) > 0, then v′(c2) < 0. Once more, the MVT tells us there exists a c ∈ (c1,c2)
such that
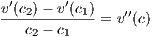
but since we’ve seen that v′(c1) > 0, v′(c2) < 0, and because c2 > c1, the above equation yields v′′(c) ≤ 0. This contradicts
the fact that v′′(x) for 0 ≤ x ≤ 1. Hence there is no point x ∈ (0,1) with v(x) > 0, and therefore v(x) ≤ 0 for all
x ∈ [0,1].
(c) Prove that ex is convex.
The second derivative of ex is ex, which is always positive. By the first part of
this problem we know that ex is convex.
(d) Prove that ex ≥ 1 + x for all x
Since the previous part of this problem showed ex is convex, then for any x,y we
have
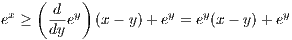
Thus, letting y = 0, we get ex ≥ x + 1 for all x.
6
(a) What constraints are on c and d so that p(x) = x3 + cx + d has three distinct real roots?
If p(x) = x3 + cx + d were to have three distinct real roots, then there would exist
real x1 < x2 where p(x1) > 0 is a local maximum and p(x2) < 0 is a local minimum. Since limx→-∞p(x) = -∞ and
limx→∞p(x) = ∞, then we can find x0,x3 ∈ ℝ with x0 < x1, x3 > x2, p(x0) < 0, and p(x3) > 0. Thus the
intermediate value theorem implies, since x1 < x2, p(x1) > 0, and p(x2) < 0, the existence of c1,c2,c3 ∈ ℝ where
x0 < c1 < x1 < c2 < x2 < c3 < x3 and p(c1) = p(c2) = p(c3) = 0. Thus it is indeed possible for there to exist three distinct
real roots.
We have that p′(x) = 3x2 + c so that x = ±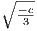 when p′(x) = 0. Hence in order for there to be three real roots, c must
be less than zero. Since x = ±
when p′(x) = 0. Hence in order for there to be three real roots, c must
be less than zero. Since x = ±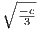 are the two local maximum and minimum, then p(
are the two local maximum and minimum, then p(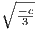 ) < 0 so that
) < 0 so that
At this point, since we have c < 0, then the right hand side of the above inequality is positive so that and this is the constraint on d.
(b) Generalize above to p(x) = ax3 + bx2 + cx + d
7
8
(a)
(b)
(c)
(d)
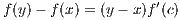
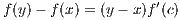

 so that g is rational, and
so that g is rational, and
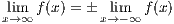
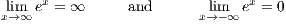
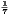 - n
- n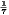 = 0
= 0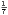 . Since this is a polynomial, it’s smooth on ℝ. For an
integer n, the mean value theorem tells us that there is an x ∈ (n,n + 1) such that
. Since this is a polynomial, it’s smooth on ℝ. For an
integer n, the mean value theorem tells us that there is an x ∈ (n,n + 1) such that


 according to the above equation. So let M =
according to the above equation. So let M = 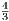 .
.
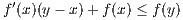
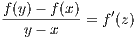
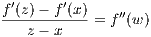
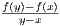 ≥ f′(x). This yields
≥ f′(x). This yields
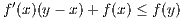
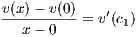
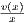 = v′(c1) which implies v′(c1) > 0 since v(x) > 0. Furthermore there exists an c2 ∈ (x,1)
where
= v′(c1) which implies v′(c1) > 0 since v(x) > 0. Furthermore there exists an c2 ∈ (x,1)
where
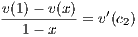
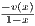 = v′(c2). Since x < 1 and v(x) > 0, then v′(c2) < 0. Once more, the MVT tells us there exists a c ∈ (c1,c2)
such that
= v′(c2). Since x < 1 and v(x) > 0, then v′(c2) < 0. Once more, the MVT tells us there exists a c ∈ (c1,c2)
such that
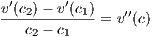
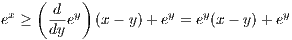
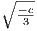 when p′(x) = 0. Hence in order for there to be three real roots, c must
be less than zero. Since x = ±
when p′(x) = 0. Hence in order for there to be three real roots, c must
be less than zero. Since x = ±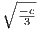 are the two local maximum and minimum, then p(
are the two local maximum and minimum, then p(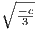 ) < 0 so that
) < 0 so that