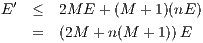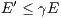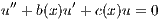Problem:

B-1

Say a function u(x) satisfies the differential equation

(1)

on the interval [0,A] and that the coefficients b(x) and c(x) are both bounded, say |b(x)|≤ M and |c(x)|≤ M (if the coefficients are continuous, this is always true for some M).

a)

Define E(x) := 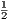(u′² + u²). Show that for some constant γ (depending on M) we have E′(x) ≤ γE(x). [Suggestion; use the inequality 2xy ≤ x² + y².]

b)

Use Problem 3(c) above to show that E(x) ≤ e^γxE(0) for all x ∈ [0,A].

c)

In particular, if u(0) = 0 and u′(0) = 0, show that E(x) = 0 and hence u(x) = 0 for all x ∈ [0,A]. In other words, if u′′ + b(x)u′ + c(x)u = 0 on the interval [0,A] and that the functions b(x) and c(x) are both bounded, and if u(0) = 0 and u′(0) - 0, then the only possibility is that u(x) ≡ 0 for all x ≥ 0.

d)

Use this to prove the uniqueness theorem : if v(x) and w(x) both satisfy equation (1) and have the same initial conditions, v(0) = w(0) and v′(0) = w′(0), then v(x) ≡ w(x) in the interval [0,A].

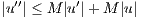
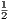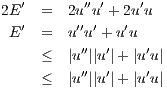
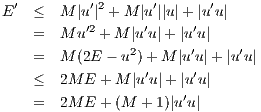
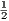Solution:

B-1

a)

From equation 1 we have u′′ = -b(x)u′- c(x)u so that |u′′| = |b(x)||u′| + |c(x)||u| which implies

(2)

Define E = (u′² + u²). Then

substituting in |u′′| from equation 2 we continue with

Since E is always positive, and E = (u′² + u²) ≥ u′u then there exists an integer n so that nE ≥|u′u|. We can there for continue as

Hence if we define the constant gamma as γ = 2M + n(M + 1) then we get

(3)

b)

As an immediate consequence of this homework’s problem 3c, equation 3 implies that E(x) ≤ e^γxE(0) for all x ∈ [0,A].

c)

d)