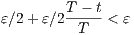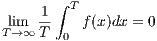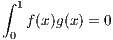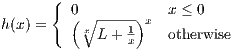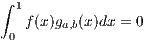Math 508: Advanced Analysis
Homework 9
Lawrence Tyler Rush
<me@tylerlogic.com>
November 14, 2014
http://coursework.tylerlogic.com/courses/upenn/math508/homework09
1
Let c ∈ ℝ be positive, f ∈ 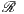 be an even function, and g ∈
be an even function, and g ∈ 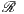 and be an odd
function.
and be an odd
function.
(a) Show ∫
-ccf(x)dx = 2 ∫
0cf(x)dx
We can separate ∫
-ccf(x)dx as
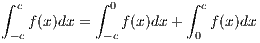
Through a change of variable, setting x = h(u) where h(u) = -u, we obtain
since f is even.
(b) Show ∫
-ccg(x)dx = 0
We can separate ∫
-ccg(x)dx as
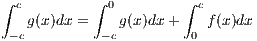
Through a change of variable, setting x = h(u) where h(u) = -u, we obtain
since g is odd.
(c) Show ∫
-ccf(x)g(x)dx = 0
Since f(-x)g(-x) = f(x)(-g(x)) = -f(x)g(x) then f(x)g(x) is an odd function.
By the previous part of this problem

2 Find function f and constant c so that ∫
0xf(t)e3tdt = c + x - cos(x2)
Let’s guess that f(t) = e-3t(1 + 2tsin(t2)) so that
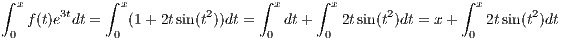 | (2.1) |
Defining g(s) = 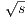 we have g(0) = 0 and g(x2
) = x so that by putting t = g(s) we have
we have g(0) = 0 and g(x2
) = x so that by putting t = g(s) we have
through a change of variable. Substituting this result back into equation 2.1 we obtain
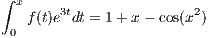
so that we see our definition of f works with c = 1.
3
Let f(x) = 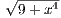 and define a partition P of [0,2] by P = {0 = x0,x1,…,xN = 2}
where xj - xj-1 = Δx = 2∕N. Since f is a monotonically increasing function on [0,2], then
and define a partition P of [0,2] by P = {0 = x0,x1,…,xN = 2}
where xj - xj-1 = Δx = 2∕N. Since f is a monotonically increasing function on [0,2], then
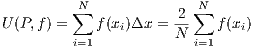
and
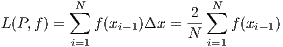
leaving us with an error in estimation of
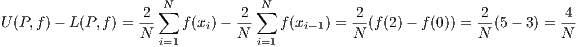
Hence, if we’d like the error in our computation of ∫
02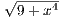 dx to be less than 1∕100, then we need 4∕N < 1∕100, i.e.
N > 400.
dx to be less than 1∕100, then we need 4∕N < 1∕100, i.e.
N > 400.
4
Let f(s) be a smooth function and c be a constant. Define
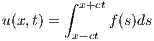
Applying the fundamental theorem of calculus then yields the following four equations
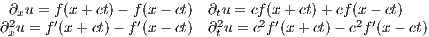
and so we see that
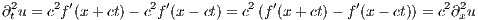
5
(a)
If we set
 | (5.2) |
then
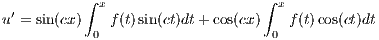
and
Hence u′′ + c2u = f(x).
(b)
Let 0 < c < 1. Let u(x) and w(x) be solutions to the differential equation
w′′ + c2w = f(x) and be zero on the boundary points of [0,π]. Then define v(x) = w(x) - u(x). We would then
have
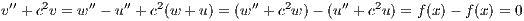 | (5.3) |
Thus the v must have the form
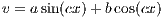
for some a and b as it is the solution of the homogenous equation in 5.3. Hence v(0) = asin(0) + bcos(0) = b = w(0) -u(0) = 0
so that b is 0. Furthermore v(π) = asin(cπ) = w(π) - u(π) = 0 so that asin(cπ) = 0. Since 0 < c < 1, then
a = 0. Thus v(x) = 0, which implies w and u are the same. Hence there is only one unique solution when
0 < c < 1.
(c)
Let c = 1, in which case we have u′′ + u = f. Thus with two applications of
integration by parts we get
(d)
Applying are result from part (a) to the situation when c = 1, the previous part
implies equation 5.2 becomes which is the unique solution for u.
6
Let L be the differential operator defined by Lw = -w′′ + c(x)w on the interval
J = [a,b], where c(x) is some continuous function. Define the inner product by
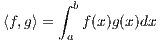
(a) Show ⟨Lu,v⟩ = ⟨u,Lv⟩ for u and v that are both zero on the boundary of J.
We first layout a helpful equation obtained via two applications of integration by
parts: taking into account that the boundary points for u and v are zero, i.e. u(a) = v(a) = u(b) = v(b) = 0. With the above
equation, our job is simple:
(b) If Lu = λ1u and Lv = λ2v for λ1≠λ2 then ⟨u,v⟩ = 0
In considering (λ1 - λ2)⟨u,v⟩, we use the previous part of this problem:
Since λ1≠λ2 we must therefore have ⟨u,v⟩.
(c) If Lu = 0 and Lv = f(x), show ⟨u,f⟩ = 0
If Lu = 0 and Lv = f, then we have the following
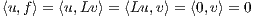
7 Compute the arclength of X(t) = (cos t, sin t,t) in ℝ3
We have that
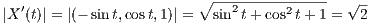
so that
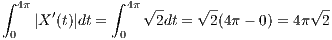
8
9
(a)
This is virtually problem 5 of the previous homework.
(b)
The value ∥f∥1 has the following three properties
- ∫
01|f(x)|dx ≥ 0 with equality only when f = 0.
- ∫
01|cf(x)|dx = |c|∫
01|f(x)|dx = |c|∥f∥
- ∫
01|f(x) + g(x)|dx ≤∫
01|f(x)| + |g(x)|dx = ∥f∥ + ∥g∥
which make it a norm on C([0,1]).
(c)
10 Compute lim λ→∞∫
01| sin(λx)|dx
Since the graph of |sin(λx)| for an arbitrary λ is just a sequence of concave “humps”,
we can find the area under a single “hump” and then multiply that times the fraction of these “humps”
that are between 0 and 1. One such “hump” is the left-most one in [0,1]. It’s area is that of the area under
|sin(λx)| on the interval [0,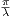 ]. Furthermore there are
]. Furthermore there are 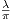 of these “humps” over the interval [0,1]. Hence we
have
of these “humps” over the interval [0,1]. Hence we
have
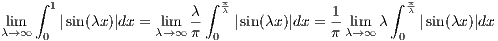
However, on the interval [0,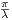 ], sin(λx) is positive and so from the above equation we get
], sin(λx) is positive and so from the above equation we get
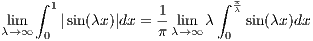
Now if we set x = g(u) where g(u) = 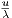 , by a change of variable, we get
, by a change of variable, we get
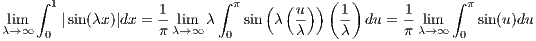
since g′(u) = 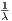 , g(π) =
, g(π) = 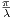 , and g(0) = 0. Hence we are left with
, and g(0) = 0. Hence we are left with
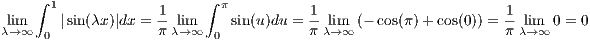
11
Define g(x) = f(x) - c. Then limx→∞ = 0 and furthermore that

Without loss of generality we may assume that c = 0. Then, since f is coninuous and limx→∞ = 0, f is bounded.
Thus there is an M such that |f(x)| < M. Let ε > 0 be given. Also becuase f is continuous, there exists a t
such that for x with 0 < t < x we have |f(x) - 0| < ε∕2. Hence we have the following sequence of equations
Thus for T such that  < ε∕2, the right-hand side of the above equation becomes
< ε∕2, the right-hand side of the above equation becomes
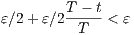
which implies
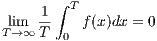
as desired.
12
(a)
Let f : [0,1] → ℝ be a continuous function such that
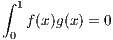
for all continuous functions g(x). In particular if g(x) = f(x) we have

Since f(x)2 ≥ 0 we must then have f(x)2 = 0, and so therefore f(x) = 0.
(b)
This is not true. By problem 6(b) of homework 6, the function
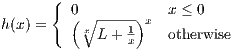
approaches L as x approaches ∞. Hence we have that the function ga,b(x) defined by h(x-a)h(b-x) is zero everywhere
except for (a,b) where a,b > 0. Furthermore g(x) ∈ C1
So, assume for later contradiction that f(x)≠0 is such that ∫
01f(x)g(x) = 0 for all g(x) in C1. Then there must be a
point x0 where f is positive. Then there exists a,b ∈ [0,1] with a < b such that x0 ∈ (a,b) and f is positive on all of (a,b).
However, since this is the case, then fga,b where ga,b is as defined above will be positive on (a,b) and zero everywhere else,
i.e.
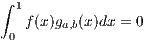
a contradiction.
 be an even function, and g ∈
be an even function, and g ∈ 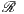 and be an odd
function.
and be an odd
function.
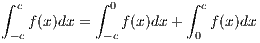

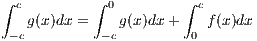
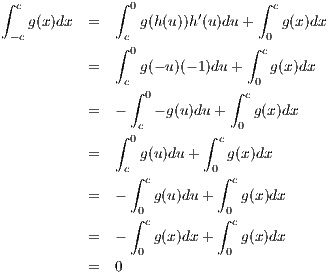

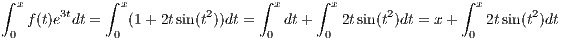
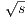 we have g(0) = 0 and g(x2
) = x so that by putting t = g(s) we have
we have g(0) = 0 and g(x2
) = x so that by putting t = g(s) we have 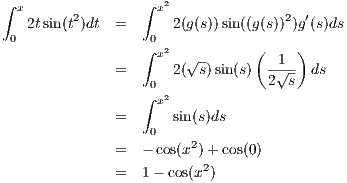
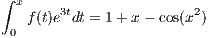
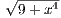 and define a partition P of [0,2] by P = {0 = x0,x1,…,xN = 2}
where xj - xj-1 = Δx = 2∕N. Since f is a monotonically increasing function on [0,2], then
and define a partition P of [0,2] by P = {0 = x0,x1,…,xN = 2}
where xj - xj-1 = Δx = 2∕N. Since f is a monotonically increasing function on [0,2], then
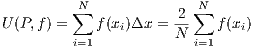
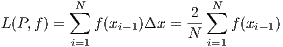
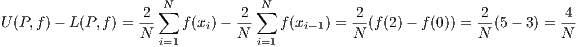
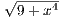 dx to be less than 1∕100, then we need 4∕N < 1∕100, i.e.
N > 400.
dx to be less than 1∕100, then we need 4∕N < 1∕100, i.e.
N > 400.
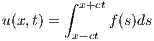
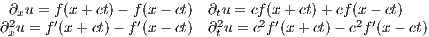
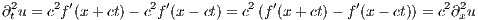

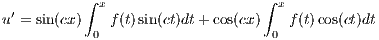
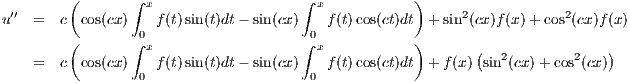
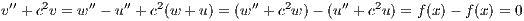
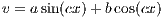
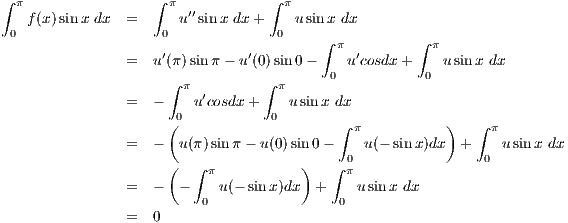
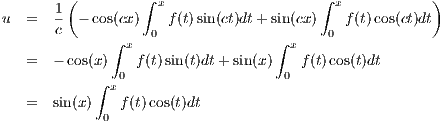
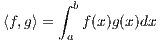
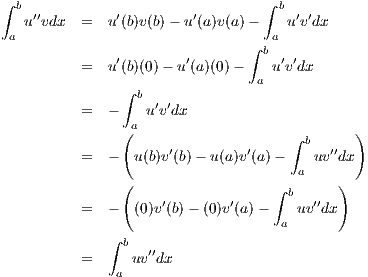
 ]. Furthermore there are
]. Furthermore there are  of these “humps” over the interval [0,1]. Hence we
have
of these “humps” over the interval [0,1]. Hence we
have
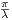 ], sin(λx) is positive and so from the above equation we get
], sin(λx) is positive and so from the above equation we get
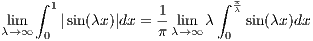
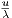 , by a change of variable, we get
, by a change of variable, we get
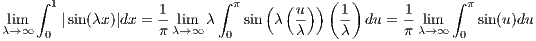
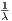 , g(π) =
, g(π) = 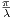 , and g(0) = 0. Hence we are left with
, and g(0) = 0. Hence we are left with
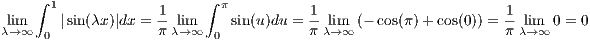


 < ε∕2, the right-hand side of the above equation becomes
< ε∕2, the right-hand side of the above equation becomes