Math 508: Advanced Analysis
Homework 10
Lawrence Tyler Rush
<me@tylerlogic.com>
November 21, 2014
http://coursework.tylerlogic.com/courses/upenn/math508/homework10
1
Let L : S → T be a linear map from vector spaces S to T. Let V 1
and V 2 be distinct solutions of the equation LX = Y 1. Futhermore let W be a solution to the equation
LX = Y 2.
(a) Find a solution to LX = 2Y 1 - 7Y 2
Put V = 2V 1 - 7W. Then

so that V is a solution to LX = 2Y 1 - 7Y 2.
(b) Find a solution (other than W) to LX = Y 2
Let V be as above and set V = V + 6W - 2V 1 + 6W so that
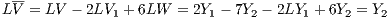
Hence V is another solution to LX = Y 2.
2
Let f(x) ∈ C([a,b]) and put
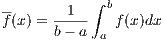
Because eu ≥ 1 + u for all u, then in particular we have ef-f ≥ 1 + f -f. Thus we have the following sequence
giving us the desired result.
3
4 Determine which of the following are pointwise and uniformly convergent
Since uniform convergence implies pointwise convergence, the proofs below omit any
mention of pointwise convergence if the given sequence is proven to be uniformly convergent.
(a) fn(x) = 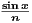 on ℝ
on ℝ
Let ε > 0 be given. Choose integer N so that Nε > 1. Since 0 ≤|sinx|≤ 1 for all
x, then
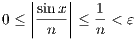
for all n ≥ N. Hence fn → 0 uniformly.
(b) fn(x) = 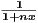 on [0, 1]
on [0, 1]
This sequence converges pointwise to
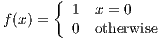
since for x = 0 fn(x) = 1 for all n. And furthermore, for any ε > 0, at a fixed x0 ∈ (0,1] we can choose integer N such that
N > 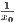
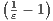 so that
so that
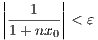
for all n ≥ N
This sequence of functions, however, does not converge uniformly. Because each fn is continuous on [0,1],
converging uniformly would imply that f above is continuous, but it’s not, due to the simple discontinuity at
x = 0.
(c) fn(x) = 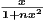 on ℝ
on ℝ
For each n,
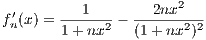
which is zero only at x = ±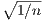 . Since fn(x) is positive on (0,∞) and negative on (-∞,0), we have that fn
has a minimum at -
. Since fn(x) is positive on (0,∞) and negative on (-∞,0), we have that fn
has a minimum at -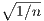 and a maximum at
and a maximum at 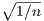 . Because the minimum and maximum for each n are
fn(-
. Because the minimum and maximum for each n are
fn(-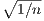 ) = -1∕2
) = -1∕2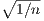 and fn(
and fn( ) = 1∕2
) = 1∕2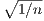 , respectively, we have
, respectively, we have
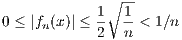
for all n ∈ ℕ. Hence, given any ε > 0, choosing integer N so that Nε > 1 gives us |fn(x)| < ε for all n ≥ N and all x ∈ ℝ.
Thus fn → 0 uniformly.
5
Let {fn} and {gn} be sequences of functions in C([0,1]). fn → f and
gn → g.
(a) If both fn → f and gn → g pointwise, does fngn → fg pointwise fg?
Yes. For a fixed x0 ∈ [0,1], {fn(x0)} and {gn(x0)} are just normal sequences, and
so fn(x0)gn(x0) → f(x0)g(x0) since fn(x) → f(x) and gn(x) → g(x).
(b) If both fn → f and gn → g uniformly, does fngn → fg uniformly fg?
Let ε > 0 be given. Because all {fn} and {gn} are continuous, then their uniform
convergence implies that both f and g are also continuous. Hence f and g are bounded on [0,1]. Due to this, we can find an
M such that |f(x)|≤ M and |g(x)|≤ M. Furthermore, the uniform convergence of fn → f and gn → g we can find integer
N such that both
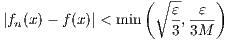
and
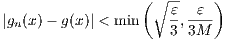
for all x ∈ [0,1] and n ≥ N. Hence we have
for all n ≥ N and all x ∈ [0,1], which implies that fngn → fg uniformly.
6
This problem is identical to a problem on the previous homework.
7 Explain which conditions of the Contracting Map Theorem fail for the following
(a) x x +
x + 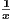 on [0,∞)
on [0,∞)
Denote this map by f. This map is not a contraction map because there is no
α < 1 such that
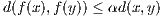 | (7.1) |
for all x,y ∈ [0,∞). This is because the difference between d(x,y) and d(f(x),f(y)) is
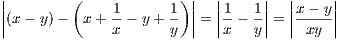
which can be made arbitrarily close to zero by making x and y large enough. This is problematic because the contraction
condition in 7.1 implies that
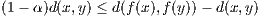
must be true; which is not the case when the difference on the righthand side above can be made arbitrarily close to
zero.
(b) x
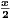 on (0, 1]
on (0, 1]
Denote this mapping by f. The failure here is that the metric space
(0,1] is not complete. In particular, the method of successive approximations fails for this mapping since the
sequence {xn} defined by xn = f(xn-1) for fixed, arbitrary x0 ∈ (0,1] converges to zero, which is not in
(0,1].
8
Let
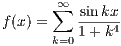
(a) For which real x is f continuous?
Define {fn} to be the partial sums of the summation f. Since |sin(kx)|≤ 1 for all
k and all x and 1 + k4 is increasing, then this sum converges for all x and therefore fn → f. Moreover, this means each fn
has a bound Mn and ∑
Mn converges. This then implies that fn → f uniformly. Hence, because each fn is continuous, f
must also be continuous.
(b) Is f differentiable? Why?
Since f(x) is a summation that converges for all x, then f(x) < ∞, and thus f(x)
is continuous since it is the composition of continuous functions. Furthermore, because
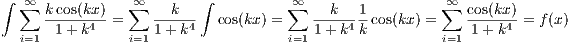
then f′(x) = 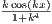 by the Fundamental Theorem of Calculus.
by the Fundamental Theorem of Calculus.
9
For any complex number z = x + iy and integer n we have nz = nx+iy = nxniy.
Furthermore we have

Thus for any sequence bounded by M and all z ∈ ℂ in the set {z = x + iy | x ≥ c} where c > 1, we have
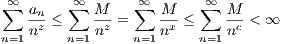
so that ∑
n=1∞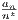 converges.
converges.
10 Show that fn(x) = n3xn(1 - x) does not converge uniformly on [0,1].
For xn = 1 - 1∕n (which is always in [0,1]) then

Therefore since (1 - 1∕n)n → 1∕e as n →∞ then fn can be made arbitrarily large and so cannot converge
uniformly.
11 Give an example of a sequence of continuous functions for each of the below.
(a) A sequence of continous functions that converges to zero on [0, 1] but not uniformly
Problem ten has already proven this.
(b)
(c)


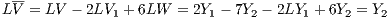
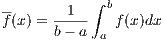
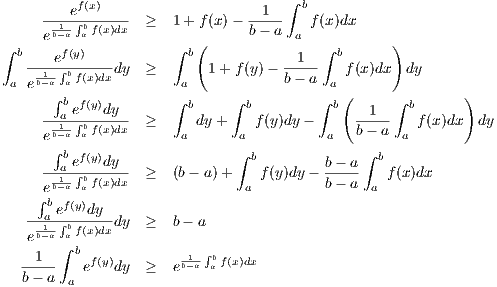
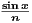 on ℝ
on ℝ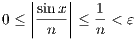
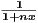 on [0, 1]
on [0, 1]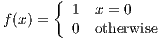
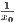
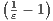 so that
so that
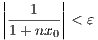
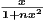 on ℝ
on ℝ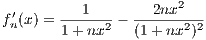
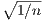 . Since fn(x) is positive on (0,∞) and negative on (-∞,0), we have that fn
has a minimum at -
. Since fn(x) is positive on (0,∞) and negative on (-∞,0), we have that fn
has a minimum at -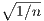 and a maximum at
and a maximum at 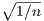 . Because the minimum and maximum for each n are
fn(-
. Because the minimum and maximum for each n are
fn(-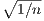 ) = -1∕2
) = -1∕2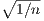 and fn(
and fn( ) = 1∕2
) = 1∕2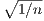 , respectively, we have
, respectively, we have
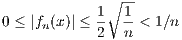
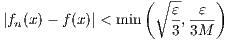
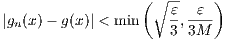
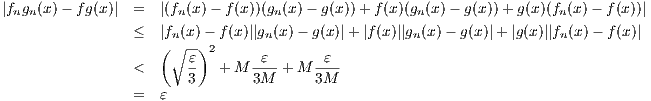
 x +
x + 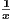 on [0,∞)
on [0,∞)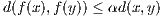
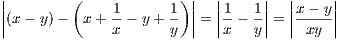
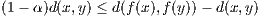

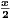 on (0, 1]
on (0, 1]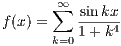
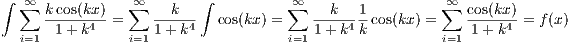
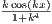 by the Fundamental Theorem of Calculus.
by the Fundamental Theorem of Calculus.

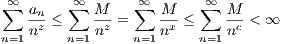
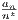 converges.
converges.


