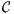Solution:

B-1

B-2

Let be the ring of continuous functions on [0,1].

a)

Let c ∈ [0,1] be fix. Define a φ : 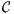→ ℝ by

Lemma 1. The function φ is a homomorphism.

Proof. The map φ preserves the operations of addition and multiplication due to

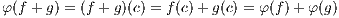
and

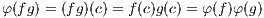
Furthermore the additive and multiplicative identities of 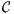are mapped to the additive and multiplicative identities of ℝ:

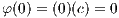
and

__

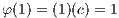
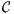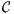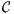With this definition of φ, we have that the kernel is exactly I = {f ∈ | f(c) = 0}. Hence with the above lemma, I is an ideal of . Futhermore, due to the above lemma and because φ is surjective (for a ∈ [0,1], the map xa is mapped to a by φ), the Fundamental Theorem of Ring Homomorphisms implies that ∕I is isomorphic to ℝ since ℝ is a field, this implies that the ideal I is a maximal ideal.

b)