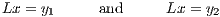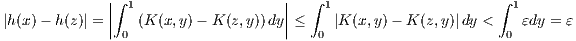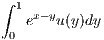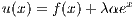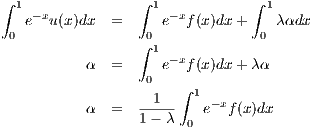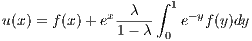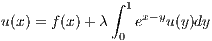Math 508: Advanced Analysis

Homework 11
Lawrence Tyler Rush
<me@tylerlogic.com>
December 4, 2014
http://coursework.tylerlogic.com/courses/upenn/math508/homework11

1

Let L : X → Y be linear map between vector spaces X and Y such that x1,x2 ∈ X are solutions, respectively, to
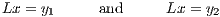
Lx = y1 and Lx = y2

for some y1,y2 ∈ Y . Furthermore, let z≠0 be a solution to Lx = 0.

(a) Find a solution for Lx = 3y1

The vector 3x1 is a solution since L(3x1) = 3(Lx1) = 3y1.

(b) Find a solution for Lx = -5y2

The vector -5x2 is a solution since L(-5x2) = -5(Lx2) = -5y2.

(c) Find a solution for Lx = 3y1 - 5y2

The vector 3x1 - 5x2 is a solution since L(3x1 - 5x2) = 3(Lx1) - 5(Lx2) = 3y1 - 5y2.

(d) Find a solution other than z and 0 for Lx = 0

The vector 2z is a solution since L(2z) = 2(Lz) = 2(0) = 0.

(e) Find two solutions of Lx = y1

Both x1 + z and x1 + 2z are solutions since L(x1 + z) = Lx1 + Lz = y1 + 0 = y1 and L(x1 + 2z) = Lx1 + 2Lz = y1 + 2(0) = y1.

(f) Find another solution to Lx = 3y1 - 5y2

The vector 3x1 - 5x2 + z is another solution since L(3x1 - 5x2 + z) = 3(Lx1) - 5(Lx2) + Lz = 3y1 - 5y2 + 0 = 3y1 - 5y2.

2

3

(a)

(b)

4

5

Since K(x,y) is continuous on [0,1] × [0,1] and [0,1] × [0,1] is compact in ℝ2, then K is uniformly continuous on [0,1] × [0,1]. Let ε > 0. Then for any x,z ∈ ℝ there exists a δ > 0 such that |x-z| < δ implies |K(x,y) - K(z,y)| < ε for all y ∈ ℝ. This implies that
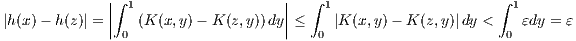
||∫ 1 || ∫ 1 ∫ 1 |h(x)- h(z)| = || (K (x,y)- K (z,y))dy|| ≤ |K (x,y)- K (z,y)|dy < εdy = ε 0 0 0

so that h is continuous.

6

If we rewrite
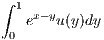
∫ 1ex-yu(y)dy 0

as αex where we define the constant α = ∫ 01e-yu(y)dy we can simplify u(x) as

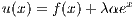x u(x) = f (x) +λ αe
(6.1)

From this simplification we have e-xu(x) = e-xf(x) + λα which, after integrating both sides with respect to x over [0,1], implies

∫ 1 -x ∫ 1 -x ∫ 1 e u(x)dx = e f(x)dx+ λ αdx 0 ∫01 0 α = e-xf(x)dx+ λα 0 ∫ --1-- 1 -x α = 1 - λ 0 e f (x)dx
Combining the last line of the above equation with equation 6.1 we end up with
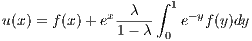
∫ x--λ-- 1 -y u(x) = f(x)+ e 1 - λ 0 e f(y)dy

Hence we have a unique solution for

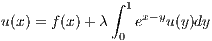
∫ 1 u(x) = f(x )+ λ ex-yu(y)dy 0

so long as λ≠0.

7

Not worded properly.

8